
Archimedes

Archimedes was, arguably, the world's greatest scientist - certainly the greatest scientist of the classical age.
He was a mathematician, physicist, astronomer, engineer, inventor, and weapons-designer. As we'll see, he was a man who was both of his time and far ahead of his time.
Archimedes was born in the Greek city-state of Syracuse on the island of Sicily in approximately 287 BC. His father, Phidias, was an astronomer.
Archimedes may also have been related to Hiero II, King of Syracuse.
Quick Guide - Archimedes' Greatest Achievements
In the 3rd Century BC, Archimedes:
invented the sciences of mechanics and hydrostatics.
discovered the laws of levers and pulleys, which allow us to move heavy objects using small forces.
invented one of the most fundamental concepts of physics - the center of gravity.
calculated pi to the most precise value known. His upper limit for pi was the fraction 22/7. This value was still in use in the late 20th century, until electronic calculators finally laid it to rest.
discovered and mathematically proved the formulas for the volume and surface area of a sphere.
showed how exponents could be used to write bigger numbers than had ever been thought of before.
proved that to multiply numbers written as exponents, the exponents should be added together.
invented the Archimedean Screw to pull water out of the ground - the device is still used around the world.
infuriated mathematicians who tried to replicate his discoveries 18 centuries later - they could not understand how Archimedes had achieved his results.
directly inspired Galileo Galilei and Isaac Newton to investigate the mathematics of motion. Archimedes' surviving works (tragically, many have been lost) finally made it into print in 1544. Leonardo da Vinci was lucky enough to see some of the hand-copied works of Archimedes before they were eventually printed.
was one of the world's first mathematical physicists, applying his advanced mathematics to the physical world.
was the first person to apply lessons from physics - such as the law of the lever - to solve problems in pure mathematics.
invented war machines such as a highly accurate catapult that stopped the Romans conquering Syracuse for years. He may have done this by understanding the mathematics of projectile trajectory.
became famous throughout the ancient world for his brilliant mind - so famous that we cannot be sure that everything he is said to have done is true.
inspired what we now believe are myths including a mirror system to burn attacking ships using the sun's rays, and jumping from his bath, then running naked through the streets of Syracuse shouting "Eureka" meaning "I've found it" after realizing how to prove whether the king's gold crown had silver in it.
Early Days and Greek Culture
The ancient Greeks were the first people to do real science and recognize science as a discipline to pursue for its own sake.
Although other cultures had made scientific discoveries, these were made for thoroughly practical reasons, such as how to build stronger temples or predict when the heavens would be right for planting crops or getting married.
Today, we would describe the Ancient Greeks' work as blue skies scientific research.
They investigated the world for the sheer pleasure of adding to their knowledge. They studied geometry for its logic and its beauty. With no practical purpose in mind, Democritus proposed that all matter was made of tiny particles called atoms and that these atoms could not be split into smaller particles. He produced logical arguments for his idea.
Archimedes was born into this Greek scientific culture. He must have felt the influence particularly strongly, flowing from his astronomer father. We believe his father was an astronomer because Archimedes says so in his work The Sand Reckoner. Writing about another astronomer's estimates of the sun's size, he says: "Pheidias, my father, said the sun was twelve times bigger".
Archimedes spent most of his life in Syracuse. As a young man he had furthered his education in the city of Alexandria in Egypt, where Alexander the Great's successor, Ptolemy Lagides, had built the world's greatest library.
The Library of Alexandria, with its meeting rooms and lecture halls, had become the focal point for scholars in the ancient world.
Some of Archimedes' work is preserved in copies of the letters he sent from Syracuse to his friend Eratosthenes. Eratosthenes was in charge of the Library of Alexandria, and was no mean scientist himself. He was the first person to calculate the size of our planet accurately.
Immersed in the scientific culture of Ancient Greece, Archimedes blossomed into one of the finest minds our world has known. He was the Einstein of his time, or perhaps we should say that Einstein was the Archimedes of his time.
An Annoying Mathematician Ignites Curiosity Far into the Future
Two thousand years after Archimedes' time, during the Renaissance and 1600s, mathematicians looked again at his work.
They knew Archimedes' results were correct, but they couldn't figure out how the great man had found them.
Archimedes was very frustrating, because he gave clues, but did not reveal his full methods. In truth, Archimedes enjoyed teasing other mathematicians. He would tell them the correct answer to problems, then see if they could solve the problems for themselves.
A Real Life Indiana Jones Style Discovery
The mystery of Archimedes' mathematics wasn't solved until 1906, when Professor Johan Heiberg discovered a book in the city of Constantinople, Turkey. (The city is now called Istanbul.)
The book was a Christian prayer book written in the thirteenth century, when Constantinople was the last outpost of the Roman Empire. Within Constantinople's walls were stored many of the great works of Ancient Greece. The book Heiberg found is now called the Archimedes Palimpsest.
Heiberg discovered that the book's prayers had been written on top of mathematics. The monk who wrote the prayers had tried to remove the original mathematical work; only faint traces of it remained.
It turned out that the traces of mathematics were actually copies of Archimedes' work - a momentous discovery. The Archimedes text had been copied in the 10th century.

A false color view of a page from the Archimedes Palimpsest, showing some of the recovered mathematics. Courtesy of The Walters Museum.
Archimedes Revealed
There were seven treatises from Archimedes in the book including The Method, which had been lost for many, many centuries.
Archimedes had written The Method to reveal how he did mathematics. He'd sent it to Eratosthenes to be lodged in the Library of Alexandria. Archimedes wrote:
"I presume there will be some current as well as future generations who can use The Method to find theorems which we have not discovered."
And so twentieth century mathematicians learned just how far ahead of his time Archimedes had been. He had summed series; he had used his discoveries in physics - the law of the lever and how to find centers of gravity - to discover new theorems in pure mathematics; and he had using infinitesimals to do work as close to integral calculus as anyone would get until Newton finally got there 1,800 years later.
Archimedes' Famous Discoveries and Inventions
The Archimedes' Screw
One of Archimedes' marvelous inventions is the 'Archimedean Screw.' This device is rather like a corkscrew within an empty tube. When the screw turns, water is pulled up the tube, so the screw can pull water up from a river, lake, or well.
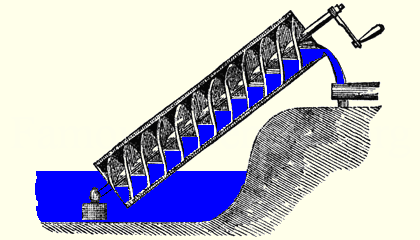
The Archimedes' Screw
Archimedes is thought to have invented this device when he was in Egypt, where it's still used for irrigation. It's also helpful for lifting light, loose materials such as ash, grain, sand from a lower level to a higher level and is still used worldwide for a variety of purposes.
The Story of the Golden Crown

Solving the Riddle of the Golden Crown
King Hiero II had given gold to a craftsman to make him a crown. The crown he got back weighed the same as the gold given to the craftsman, but King Hiero was suspicious. He thought the craftsman had stolen some gold, replacing it with silver in the crown. He couldn't be sure, so he sent for Archimedes and explained the problem to him.
It was known that gold was denser than silver, so a one centimeter cube of gold would weigh more than a one centimeter cube of silver.
The problem was that the crown was irregularly shaped, so although its weight was known, its volume wasn't.
Archimedes is believed to have measured how much the level of water in a cup was raised by sinking, for example, one kilogram of gold in it, and comparing this with one kilogram of silver.
If we did this measurement using modern equipment, we would find the 1 kg of gold would raise the water level by 51.8 ml and the 1 kg of silver by 95.3 ml.
So, if King Hiero's crown weighed 1 kg, and it raised the water level by 52 ml or so, then the crown would be pure gold. If the water level rose more than this, then some of the gold had been replaced by silver.
Archimedes found that the crown was a mixture of gold and silver, which was bad news for King Hiero, and even worse news for the King's craftsman!
Archimedes is supposed to have had the idea of how to solve King Hiero's problem when he was taking a bath, noticing the water level moving as he lowered and raised himself. He was so excited that he leaped up and ran naked through the streets of Syracuse shouting "Eureka," meaning, "I've found it." It seems that even thousands of years ago, scientists had a reputation for being a little crazy!
Calculation of Pi
p is the number you get when you divide the circumference of a circle by its diameter.
To calculate a circle's area, or circumference, you need to know p.
Archimedes was intensely interested in calculating the mathematical properties of curved solids, such as cylinders, spheres and cones. To do this, he wanted to learn more about p.
We now know that p is an irrational number: 3.14159265358979... the numbers after the decimal point follow no pattern and never end, so an exact value can never be found.
Archimedes knew that the circumference of a circle equals 2 x p x r, where r is the circle's radius.
Here is how Archimedes calculated the circumference of a circle of known radius, and hence found p.
He imagined a circle, and in his mind drew an equilateral triangle inside it, with each point of the triangle touching the circle. Outside the circle, he drew another equilateral triangle, with each side touching the circle.
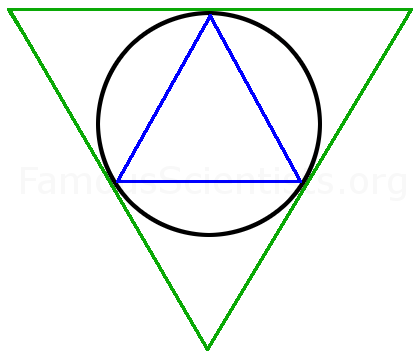
Archimedes drew a mental image of a circle bounded by triangles.
He could easily calculate the perimeter of each triangle, and therefore he knew the circle's circumference was greater than the inside triangle and smaller than the outside triangle.
Then, using a formula he had devised to calculate the perimeter of a polygon with double the number of sides of the previous polygon, he repeated his calculation, this time for a circle with a regular hexagon inside it, and a regular hexagon outside it. The hexagons enclosed the circle more closely than the triangles had and their perimeters were nearer to the true circumference of the circle.
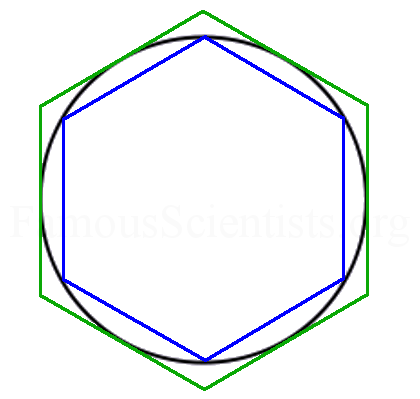
Archimedes drew a mental image of a circle bounded by regular hexagons.
In this way Archimedes tightened the limits for the maximum and minimum circumference of the circle. Next, he imagined a circle between two 12-sided regular polygons, then two 24-sided regular polygons, then two 48-sided regular polygons. Finally, Archimedes calculated the circumference of a 96-sided regular polygon inside his circle, and a 96-sided regular polygon outside his circle. A 96-sided regular polygon looks the same as a circle unless you zoom in with high magnification.

Above is a 90-sided polygon. It has fewer sides than the 96-sided polygon Archimedes used for his calculation, but you can see that it looks like a circle to the human eye.
Using the 96-sided polygon, Archimedes found that p was greater than the fraction 25344/8069, and less than the fraction 29376/9347.
For the world at large, he simplified these numbers, losing a tiny amount of precision to say p was bigger than 310/71 and smaller than 31/7.
If we average Archimedes' best upper and lower limits for p, we get it to be 3.141868115 to nine decimal places. Archimedes' value of p differs from the value on your calculator by less than 1 part in 10,000.
In fact, Archimedes' value of p of 31/7 (this is often written as 22/7) was used extensively until it entered a graceful retirement in our digital age.
Remember that Archimedes did not actually make measurements for his calculations. They could never have been precise enough. He used pure mind-power to calculate the areas involved in each situation.
Calculation of the Volume of a Sphere
Archimedes saw his proof of the volume of a sphere as his greatest personal achievement. His work is remarkable for its similarity to modern calculus.
Archimedes gave instructions that his proof should be remembered on his gravestone.
For details click here: "Calculation of the Volume of a Sphere"
The Beast Number
Read about how Archimedes invented the Beast Number, a number so enormous that the visible universe isn't big enough to write it out in full.
And all this because he was fed up of people saying that it was impossible to calculate how many grains of sand there were on a beach.
For details click here: "How Archimedes Invented the Beast Number"
Death and Legacy
Archimedes died during the conquest of Syracuse in 212 BC when he was killed by a Roman soldier.
He was buried in a tomb on which was carved a sphere within a cylinder. This was his wish, because he believed his greatest achievement was finding the formula for the volume of a sphere.
Many years later, Cicero, the Roman Governor of Sicily, went looking for the tomb of Archimedes.
He found that it had become overgrown with weeds and bushes, which he ordered to be cleared.
Today we do not know where Archimedes' tomb is - it has been lost, probably for ever.
Much of his work has also been lost for ever, but what we know of it leaves us in awe of his achievements from so long ago.
More than 300 years after Archimedes' death the Greek historian Plutarch said of him:
"He placed his whole affection and ambition in those purer speculations where there can be no reference to the vulgar needs of life."
Archimedes was a great practical scientist, but above all, he lived up to the Greek ethos of carrying out blue sky research. He worked on mathematical problems for the sake of mathematics itself, not to solve practical problems. Funnily enough, all of his discoveries in mathematics ultimately did prove to be useful both practically as well as mathematically.
On his tomb, in addition to the sphere in the cylinder, his name was written in Greek:

[1]
Sources
Our Mobile Application
Check out Our Mobile Application "Ancient Greece Reloaded"


