Ancient Greece Reloaded

ANCIENT GREECE RELOADED

ENTER THE WORLD OF MYTHS AND LEGENDS

Heron of Alexandria

Heron of Alexandria (Greek: Ἥρων ὁ Ἀλεξανδρεύς, Heron ho Alexandreus; also known as Hero of Alexandria c. 10 – c. 70 AD) was a Greek mathematician and engineer who was active in his native city of Alexandria, Roman Egypt. He is considered the greatest experimenter of antiquity and his work is representative of the Hellenistic scientific tradition.

The ancient invention of the steam engine by the Hero of Alexandria

In our society today we are often surprised and impressed by the advancement of technology and engineering, a major characteristic of our civilisation. However if we look back more than 2,000 years ago, we can find mechanical marvels and incredible feats of engineering that were ahead of their time. Many became lost to the pages of history, only to become reinvented just a few centuries ago. This includes the first modern of the steam engine.

Heron Alexandrinus, or Hero of Alexandria as he was often known, was a Greek born in 10AD in Alexandria, now part of Egypt, and the second largest city after Cairo. Little is known about the life of Heron, however, we are aware that he was born to Greek parents that migrated to Alexandria after the conquest of Alexander the Great. Heron was a mathematician and an engineer considered to be one of the greatest inventors of ancient times.

During the era in which Heron lived, the great Library of Alexandria was in its glory and Heron is believed to have taught at the Museum of Alexandria, a place for scientists and scholars to meet and discuss.

What very few people know, thanks to the omission of important facts from our history books, is that Heron was the first inventor of the steam engine , a steam powered device that was called aeolipile or the ‘Heron engine’. The name comes from the greek word ‘Aiolos’ who was the Greek God of the winds.

Although a few others have talked about devices similar to aeolipiles before Heron, Heron was the first one to describe them in detail and give instructions for manufacturing them in his book Pneumatica, where more than 78 devices are described. Many of Heron’s ideas were extensions and improvements of another Greek inventor who lived in Alexandria 300 years before him, known as Ktesibios, the first to write about the science of compressed air.

But what is an aeolipile? It is a sphere that is positioned in such a way that it can rotate around its axis. Nozzles that are opposite to each other would expel steam and both of the nozzles would generate a combined thrust resulting in torque, causing the sphere to spin around its axis. The rotation force speeds up the sphere up to the point where the resistance from traction and air brings it to a stable rotation speed. The second video at the end of this article demonstrates how it works.

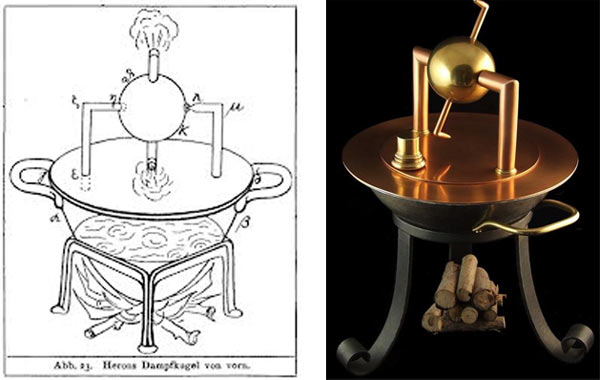
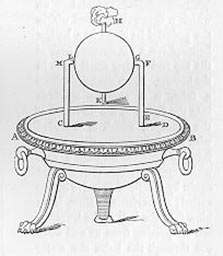
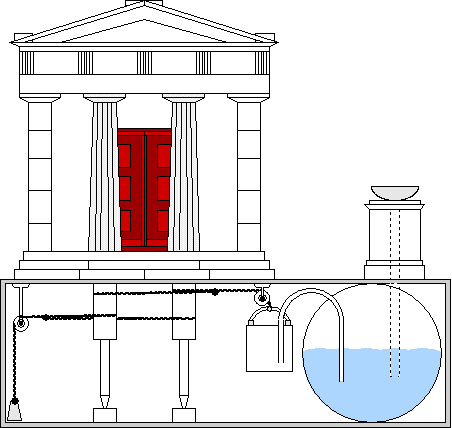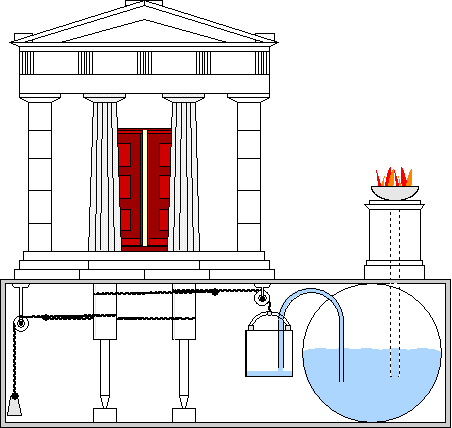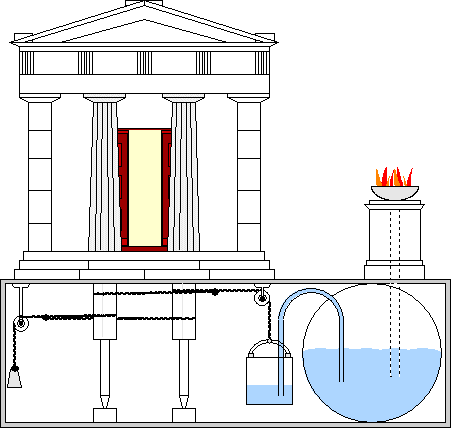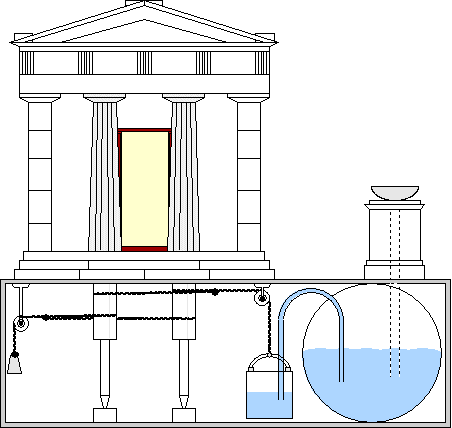
The steam was created by boiling water either inside the sphere or under it, as seen in the image. If the boiler is under the sphere, then it is connected to the rotating sphere through a pair of pipes that at the same time serve as pivots for the sphere. The replica of Heron’s machine could rotate at 1,500 rounds per minute with a very low pressure of 1.8 pounds per square inch.

PLACE a cauldron over a fire: a ball shall revolve on a pivot. A fire is lighted under a cauldron, A B, (fig. 50), containing water, and covered at the mouth by the lid C D; with this the bent tube E F G communicates, the extremity of the tube being fitted into a hollow ball, H K. Opposite to the extremity G place a pivot, L M, resting on the lid C D; and let the ball contain two bent pipes, communicating with it at the opposite extremities of a diameter, and bent in opposite directions, the bends being at right angles and across the lines F G, L M. As the cauldron gets hot it will be found that the steam, entering the ball through E F G, passes out through the bent tubes towards the lid, and causes the ball to revolve, as in the case of the dancing figures. Heron, Pneumatica

This invention was forgotten and never used properly until 1577, when the steam engine was re-invented by the philosopher, astronomer and engineer, Taqu al-Din. But he basically described the same device as Heron, a method for rotating a spit by using jets streams on the periphery of a wheel.

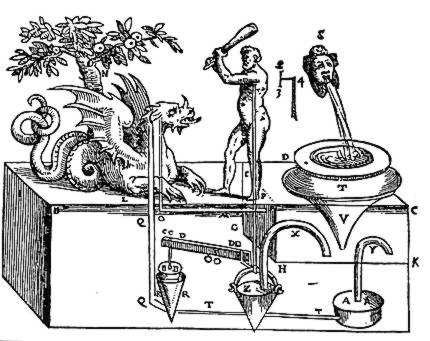
Reconstruction of one of many “automata” of Heron by Giovanni Battista Aleoti 1589. Hercules and the Dragon. When Hercules hits the head of the dragon the dragon shoots water on his face.

Another invention of Heron was the ‘wind wheel’, a wind-driven wheel that was used to power a machine that was connected to a pipe organ. He also invented the first vending machine, automatic opening doors, ‘miraculous’ movements and sounds in temples, a fire engine, a standalone fountain, and many of the mechanisms of the Greek theatre. One of his theatrical mechanical inventions included a completely mechanical robotic theatrical play by using a binary system of knots and ropes and simple machines, even creating artificial sounds of thunder, pumps and concentration of light to specific parts of the performance. His works include descriptions of machines working on air, steam or water pressure, architectural devices for lifting heavy objects, methods of calculating surfaces and volumes – including a method of calculating the square root, war machines, and manipulation of light using reflection and mirrors.

Animated Image by P. Hausladen, RS Vöhringen

It is clear that Heron was a genius with knowledge that was incredibly advanced for the time. Unfortunately, most of his original writings have been lost, with just a few surviving in Arabic Manuscripts. Who knows how many more incredible inventions were documented by Heron more than 2,000 years ago.

[1]

John F. BROCK in Pyramids to Pythagoras: Surveying from Egypt to Greece – 3000 B.C. to 100 A.D. gives a description of the content of Heron's Dioptra book:

1) and 2) Introduction to “the science of dioptrics”.

3) and 4) Instructions on how to construct a dioptra instrument.

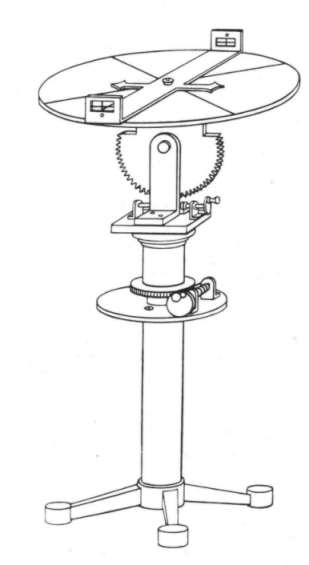
Reconstruction of Heron's dioptra from Schöne, Hero Alexandrinus. Heronis Alexandrini opera quae supersunt omnia. Vol. III: Rationes dimetiendi et commentation dioptrica. Griechisch und Deutsch H. Schöne. - Leipzig: B. G. Teubner, 1903.

5) Instructions on how to produce a stave for measurement.

6) To observe the difference in height between two points or if their height is the same.

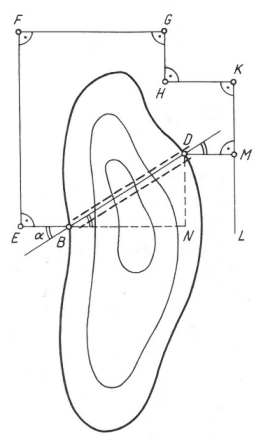
Example by Heron how to use the Dioptra to construct a tunnel through two opposite points in a mountain. Take a point close to the first entrance B and another point E. Then use the Dioptra to obtain the perpendicular line EF and through a set of other perpendicular segments get line segment KL the point M for which DM is perpendicular to KL, where D is the other opposite entrance point. Using DN and NB estimate the angle alpha necessary to connect points B and D. The tunnel of Eupalinos shows that even 500 years before the Greeks have the knowledge and devices to produce such tunnels.

7) To draw a straight line by dioptra from a given point to another invisible point, whatever the distance between them.

8) To find the horizontal (pros diabeten) interval between two given points, one near us, the other distant, without approaching the distant one.

9) To find the minimum width of a river while staying on the same bank.

10) To find the horizontal interval between two visible but distant points, and their direction.

11) To find a line at right angles at the end of a given line, without approaching either the line or its end.

12) To find the perpendicular height of a visible point above the horizontal plane drawn through our position, without approaching the point.

13) (a) To find the perpendicular height of one visible point above another, without approaching either point. (b) To find the direction of a line connecting two points, without approaching them.

14) To find the depth of a ditch, that is the perpendicular height from its floor to the horizontal plane either through our position or through any other point.

15) To tunnel through a hill in a straight line, where the mouths of the tunnel are given.

16) To sink shafts for a tunnel under a hill, perpendicular to the tunnel.

17) To lay out a harbour wall on a given segment of a circle between given ends.

18) To mound up the ground in a given segment of a spherical surface.

19) To grade the ground at a given angle, so that on a level site with the shape of an equal-sided parallelogram its gradient slopes to a single point.

20) To find a point on the surface above a tunnel so that a auxiliary shaft can be sunk.

21) To lay out with the dioptra a given distance in a given direction from us.

22) To lay out with the dioptra a given distance from another point, parallel to a given line, without approaching the point having the line on which to lay it out.

23) to 30) The first five chapters refer to the dioptra setting out irregular shaped plots of land, while the remaining three explain how to determine the areas from those figures.

31) To measure the discharge or outflow of a spring.

32) and 33) Describes how to utilize the dioptra in a vertical mode for the purposes of astronomical observations.

34) This chapter informs the reader about the usage of another measuring instrument called the odometer, which has a device fitted to the wheels of a carriage such that the horizontal distance is evaluated in a very similar fashion to which a modern day perambulator gives distance

[2]