Hippasus
HIPPASUS OF METAPONTUM (fl. 5th century BC), was a Pythagorean philosopher . Little is known about his life or his beliefs, but he is sometimes credited with the discovery of the existence of irrational numbers.
The discovery of irrational numbers is said to have been shocking to the Pythagoreans, and Hippasus is supposed to have drowned at sea, apparently as a punishment from the gods for divulging this. However, the few ancient sources which describe this story either do not mention Hippasus by name (e.g. Pappus) or alternatively tell that Hippasus drowned because he revealed how to construct a dodecahedron inside a sphere.
The discovery of irrationality is not specifically ascribed to Hippasus by any ancient writer. Some modern scholars though have suggested that he discovered the irrationality of √2, which is believed to have been discovered around the time that he lived.
[1]
The Legend of Hippasus
There was once an ancient Greek geometer named Hippasus who belonged to the Pythagorean Brotherhood. The Pythagoreans were a school of philosophers who held a special reverence for numbers and proportion. To these men, mathematics was more than just a method for quantifying and describing the world around them. The Pythagoreans held that numbers, themselves, were divine things, worthy of awe and worship. Relationships between these numbers - what we would now think of as a "proportion" or "ratio" of numbers - were intensely studied, as these proportions were thought to hold the secrets of the cosmos. If one were to divide a string according to some specific ratios, he could produce beautiful music. If one compared the proportions of two legs of a triangle, he could come to understand the remaining leg. Nothing in existence was more beautiful to the Pythagoreans than the discovery of these proportions and the properties they endowed.
Occasionally in their calculations, the Pythagoreans would happen upon a proportion that was mysterious, to them. Discovering the exact ratio of numbers between these mysterious proportions was a delight and a treasure for members of the Brotherhood. Such finds were celebrated and lauded, and therefore these mysteries were pursued with diligent hearts. Hippasus was working on just such a problem. The particular case that Hippasus was attempting to resolve was actually a very common proportion, but its exact calculation had stumped many great minds for quite a long time. If he could discover the ratio behind this proportion, he would be guaranteed fame and glory amongst his brethren. So, Hippasus dedicated himself entirely to this pursuit, not even resting from his work while he travelled. And it just so happened that, while sailing across the Mediterranean, Hippasus discovered his answer.
But, it was not the answer he had expected.
Hippasus had been trying to find a ratio between two numbers which would describe his problematic proportion; but the answer that he discovered was that no such ratio could possibly exist. The number was, quite literally, irrational. This discovery was revolutionary. One of the principle tenets of the Pythagorean philosophy was the fundamental universality of these ratios. According to their beliefs, everything in the universe should be able to be described as a ratio between two numbers. And here, Hippasus had proven that there existed certain proportions which could not possibly be described rationally. Excited and thrilled at his discovery, Hippasus sprinted across the deck of the ship, yelling to his brothers about his breakthrough. But when they heard his claim, the Pythagoreans were appalled. In their eyes, Hippasus was not only preaching heresy, he had definitively PROVEN his heretical claim. Where Hippasus had expected to be met with praise and celebration, he instead found fear and denial and anger. The other Pythagoreans soon built into a murderous rage, and their curious brother became the target of their ire.
For the transgression of discovering the truth, Hippasus was thrown overboard and drowned in the waters of the Mediterranean Sea.
Now, this legend likely never actually happened, historically. The tale I've told expands quite a bit above and beyond what can be pieced together from ancient historians, and even those bits which I've accurately retold remain dubious, at best. But, as in any parable, the truth to be found in this story has nothing at all to do with whether or not it actually occurred, as written. There is a moral - a meaning to be discovered - in the text of the tale. And in the case of poor Hippasus, I have attempted to illustrate the dangers of constructing dogmatic views of reality based upon unjustified beliefs.
When we attempt to assert how the universe must be structured, rather than attempting to learn how it truly is, we might as well be drowning Hippasus ourselves.
[2]
On the Irrationality of the Square Root of 2
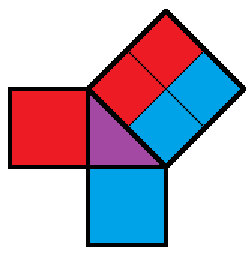
Consider a triangle with two legs of equal length which meet at a right angle. What is the proportion of the length of the Hypotenuse to the length of one Leg?
Let us assume that there exists some ratio of two whole numbers H/L which represents the proportion we seek, exactly. Let us further assume that this ratio is in simplest form, such that H and L share no common factors. What can we know about H? According to the Pythagorean Theorem, we know that the square on the Hypotenuse is equal to the sum of the squares on the Legs. We also know that adding a number to itself, regardless of whether that number is odd or even, always yields an even sum. Therefore, since the squares on the Legs are equal, we know that the square on the Hypotenuse must be an even number. And since the square root of an even number is always even, we know that the Hypotenuse, itself, must be an even number.
Therefore, H is even.
What, then, can we know about L? Since we know that the square on one of the Legs is equal to half of the square on the Hypotenuse, we can know that the square on the Leg must be an even number, as well. After all, dividing an even square number by 2 always yields an even number. And, again, if the square on the Leg is even, its root must also be even, so we know that the Leg is an even number.
Therefore, L is even.
However, if both H and L are even, they must share a common factor of 2. Since our initial assumption was that our ratio, H/L, was in simplest form, we have reached a contradiction. A ratio cannot be in simplest form if its constituents share common factors.
We can therefore conclude that there exists no ratio of whole numbers which can represent the proportion of the Hypotenuse to the Leg of this triangle. That proportion must be Irrational.
[3]
Sources
[1] "The Info List" by Stephen Payne
[2] "Boxing Pythagoras"
[3] "Boxing Pythagoras"













