Oenopides of Chios
Oenopides of Chios (Greek: Οἰνοπίδης) was an ancient Greek mathematician (geometer) and astronomer, who lived around 450 BCE. He was born shortly after 500 BCE on the island of Chios, but mostly worked in Athens.
Very little is known about the life of Oenopides of Chios except that his place of birth was the island of Chios. We believe that Oenopides was in Athens when a young man but there is only circumstantial evidence for this.
In Plato's Erastae Oenopides is described as (see for example [1]):
... having acquired a reputation for mathematics...
and Plato also describes a scene where Socrates comes across two young men in the school of Dionysius who was Plato's teacher. The young men were discussing a question in mathematical astronomy which had been tackled by Oenopides and Anaxagoras. This question was certainly that of the angle that the ecliptic makes with the celestial equator. Bulmer-Thomas writes in [1]:
... it was probably [Oenopides] who settled on the value of 24°, which was accepted in Greece until refined by Eratosthenes. Indeed, if Oenopides did not fix on this or some other figure it is difficult to know in what his achievement consisted, for the Babylonians no less than the Pythagoreans and Egyptians must have realised from early days that the apparent path of the sun was inclined to the celestial equator.
However, in contrast to these claims, Heath writes [2]:
It does not appear that Oenopides made any measurement of the obliquity of the ecliptic.
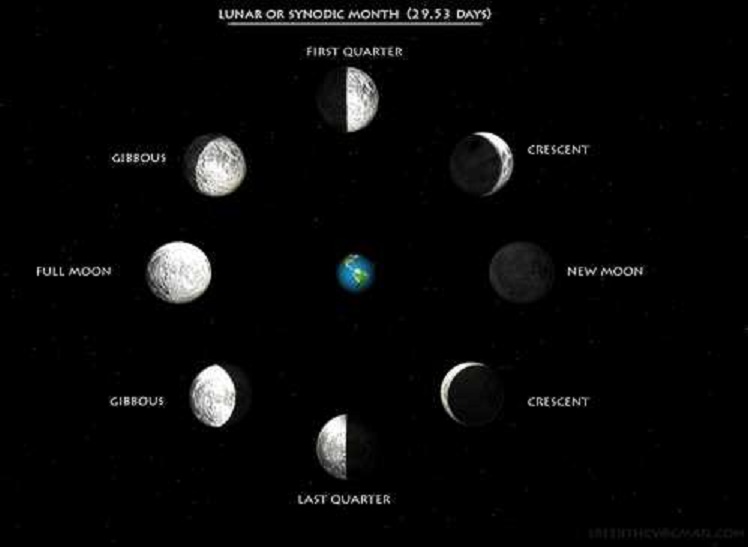
Another major contribution to mathematical astronomy made by Oenopides was his discovery of the period of the Great Year. Originally the "Great Year" was the period after which the motions of the sun and moon came to repeat themselves. Later it came to mean the period after which the motions of the sun, moon and planets all repeated themselves so in the period of one Great Year all should have returned to their positions at the beginning of the Great Year.
Oenopides gave a value of the Great Year as 59 years. Heath writes [2]:
His Great Year clearly had reference to the sun and moon only; he merely sought to find the least integral number of complete years which would contain an exact number of lunar months.
Based on this Paul Tannery [5] showed that Oenopides' result leads to a lunar month of 29.53013 days which is remarkably close to the modern value of 29.53059 days. However many historians doubt whether Oenopides could have collected sufficient good quality data to enable him to obtain a value as accurate as this. To collect the data for even one period requires 59 years and this makes it almost impossible for someone to gather the data in their own lifetime.
Toomer believed that in fact despite Oenopides' Great Year of 59 years, he did not have this accurate value for the length of the month, and later calculations were made using better data than would have been available to Oenopides to give this very accurate value for the length of the month, more accurate than Oenopides could ever have known.
Paul Tannery in [5] makes another claim however when he states that Oenopides considered some of the planets as well as the sun and moon as part of his 59 year Great Year. The data works well for some of the planets, for example Saturn is only 2° from its starting position at the end of the 59 year cycle. Tannery is forced to conclude that not all the planets could have been taken into account by Oenopides, however, as some of the planets would be in the wrong sign of the Zodiac after the period ended.
Proclus attributes two theorems which appear in Euclid's Elements to Oenopides. These are to draw a perpendicular to a line from a given point not on the line, and to construct on a line from a given point a line at a given angle to the first line. These are elementary results but Heath believes that their significance might be that Oenopides set out for the first time the explicit 'ruler and compass' type of allowable construction. He writes [2]:
... [Oenopides] may have been the first to lay down the restriction of the means permissible in constructions with ruler and compasses which became a canon of Greek geometry for all plane constructions...
Oenopides also developed a theory to account for the Nile floods. He suggested that heat stored in the ground during the winter dries up the underground water so that the river shrinks. In the summer the heat disappears, as testing the temperature of deep wells suggests, and water flows up into the river so causing floods. This theory, which of course is false, did not prove popular as other rivers in Libya were subject to similar conditions but did not behave in the same way.
We have some other indications of the philosophy of Oenopides. He is said to have believed in fire and air as basic elements and thought of the world as a living being with God as its soul.
References for Oenopides
1. I Bulmer-Thomas, Biography in Dictionary of Scientific Biography (New York 1970-1990).
Books:
2. T L Heath, A history of Greek mathematics I, II (Oxford, 1931).
3. D R Dicks, Early Greek Astronomy to Aristotle (London, 1970).
Articles:
4. J Mau, Oinopides, in Der Kleine Pauly IV (Stuttgart, 1972), cols. 263-264.
5. P Tannery, La grande année d'Aristarque de Samos, Mémoires de la Société des sciences physiques et naturelles de Bordeaux 4 (1888), 79-96.
[1]
Sources
[1] "School of Mathematics and Statistics University of St Andrews, Scotland" by J J O'Connor and E F Robertson
Oenopides of Chius A survey of the modern literature with a collection of the ancient testimonia, Berlin2007 - István M. Bodná
Get the research from our Online-library:
"Here"