ΔΕΙΝΟΣΤΡΑΤΟΣ
Ο Δεινόστρατος (~390-310 π.Χ) ήταν Έλληνας μαθηματικός της κλασικής αρχαιότητας, συνεργάτης του Πλάτωνα και επιφανές μέλος της Ακαδημίας.
Βιογραφικά Στοιχεία
Ο Δεινόστρατος γεννήθηκε περίπου το 390 π.Χ. στην Προκόννησο της Προποντίδας και ήταν αδελφός του Μέναιχμου. Μαζί με τον αδελφό του εγκαταστάθηκε στην Αθήνα όπου έζησε όλη την υπόλοιπη ζωή του. Αρχικά μαθήτευσε κοντά στον Εύδοξο τον Κνίδιο και αργότερα έγινε μέλος της Ακαδημίας του Πλάτωνα και συνεργάτης του Πλάτωνα, με τον οποίο συνδέθηκε φιλικά.
Το μαθηματικό του έργο
Ο Δεινόστρατος μαζί με τον Θεαίτητο, τον Λεωδάμαντα τον Θάσιο, τον Εύδοξο, τον Μέναιχμο και τον Θεύδιο εργάστηκαν εντατικά εντός της Ακαδημίας και η συνεισφορά τους στη μαθηματική επιστήμη ήταν μεγάλη.
Στον Δεινόστρατο αποδίδεται από τον Πάππο μια λύση (~350 π.Χ) για τον τετραγωνισμό του κύκλου με τη βοήθεια μιας καμπύλης που ονομάζεται Τετραγωνίζουσα.
Επίσης ασχολήθηκε με την αστρονομία και τη μουσική.
Τετραγωνισμός του κύκλου - Η λύση του Δεινόστρατου
Στην μεγάλη επιτομή του Πάππου, η οποία πρέπει να γράφτηκε στην εποχή του αυτοκράτορα Διοκλητιανού (284-305 μ.Χ.),αναφέρεται ότι ο Δεινόστρατος, ο αδελφός του Μεναίχμου και ο Νικομήδης χρησιμοποίησαν για τον τετραγωνισμό του κύκλου μια καμπύλη, η οποία για τον λόγο αυτό ονομάστηκε τετραγωνίζουσα . Την καμπύλη αυτή την ανακάλυψε ο Ιππίας φαίνεται όμως ότι ο Δεινόστρατος την χρησιμοποίησε για τον τετραγωνισμό του κύκλου. (Την τετραγωνίζουσα έχουμε περιγράψει στο πρόβλημα της τριχοτόμησης της γωνίας –η λύση του Ιππία )
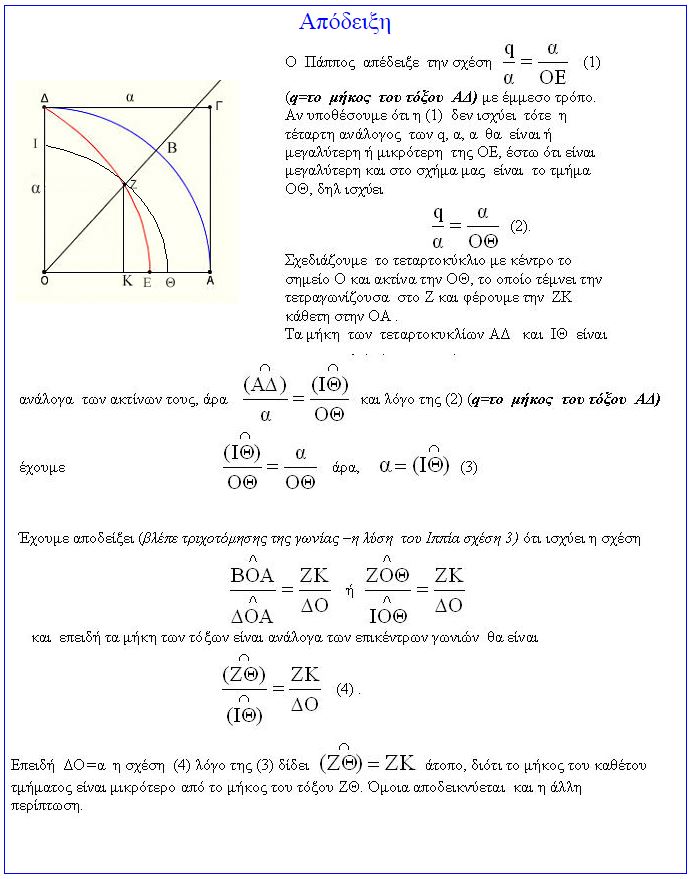
Στο παρακάτω σχήμα έχουμε ένα τετράγωνο ΟΑΓΔ, ένα ημικύκλιο ΑΔ και την τετραγωνίζουσα ΔΕ. Ονομάζουμε q = το μήκος του τόξου ΑΔ
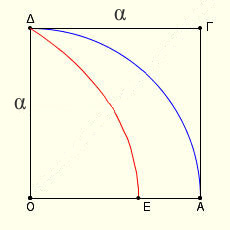
Ο Πάππος, ενδεχόμενα ο ίδιος ο Δεινόστρατος (γύρω στο 350 π.Χ.), απέδειξε ότι
( "δες απόδειξη" ):
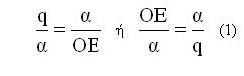
Από την (1) προκύπτει ότι το μήκος q του τεταρτοκυκλίου ΑΔ κατασκευάζεται ως τέταρτη ανάλογος των α,α ( το τμήμα α είναι η ακτίνα του κύκλου στον οποίο ανήκει το τόξο) και του μήκους ΟΕ, όπου Ε είναι το σημείο στο οποίο η τετραγωνίζουσα τέμνει την ΟΑ. Μπορούμε τώρα να κατασκευάσουμε ένα ευθύγραμμο τμήμα με μήκος 4q, δηλ ίσο με το μήκος του κύκλου.
Ο Δεινόστρατος προφανώς γνώριζε την πρόταση που απέδειξε αργότερα ο Αρχιμήδης ότι:
Το εμβαδόν ενός κύκλου είναι ίσο με το εμβαδόν ενός ορθογωνίου τριγώνου, που η μία από τις κάθετες πλευρές του είναι ίση με το μήκος του κύκλου και η άλλη με το μήκος της ακτίνας του.
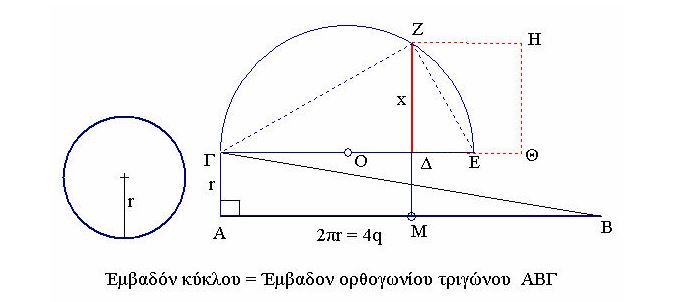
Έτσι για να τετραγωνίσουμε τον κύκλο ακολουθούμε τα παρακάτω βήματα:
σχηματίζουμε ένα ορθογώνιο τρίγωνο ΑΒΓ με κάθετες πλευρές ΑΓ= r και ΑΒ = 4q.
παίρνουμε το μέσο Μ της ΑΒ και σχηματίζουμε το ορθογώνιο ΑΜΔΓ του οποίου το εμβαδό θα είναι ίσο με το εμβαδόν του τριγώνου.
προεκτείνουμε την ΓΔ και παίρνουμε τμήμα ΔΕ = ΔΜ, κατασκευάζουμε το ημικύκλιο με διάμετρο την ΓΕ, στο σημείο Δ φέρουμε την κάθετη ΔΖ προς την ΓΕ και το τμήμα ΔΖ είναι η πλευρά x του ζητούμενου τετραγώνου
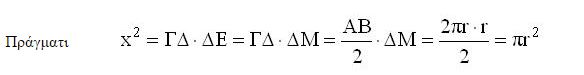
Βιβλιογραφια - Πηγες
[1] "Wikipedia"
[2] "users.sch"
Πάππος ο Αλεξανδρεύς, "Μαθηματική Συναγωγή", Εκδόσεις Αίθρα, Αθήνα 2003
Σωτήρης Χ. Γκουντουβάς, "Γεωμετρικές Διαδρομές", Αθήνα 2015
Thomas Heath, "Ιστορία των Ελληνικών Μαθηματικών", ΚΕΠΕΚ, Αθήνα 2001
Β. L. Van der Waerden, "H αφύπνιση της επιστήμης", ΠΕΚ, Ηράκλειο 2003