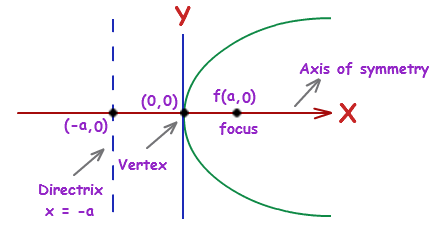
ΔΙΟΚΛΗΣ Ο ΑΛΕΞΑΝΔΡΕΥΣ
Ο Διοκλής ο Αλεξανδρεύς (περ. 240 π.Χ. - περ. 180 π.Χ.) ή Διοκλής ο Καρύστιος, ήταν αρχαίος Έλληνας μαθηματικός και γεωμέτρης.
Βίος και έργο
Ο Διοκλής έζησε την εποχή του Απολλώνιου και άκμασε στο τέλος του 3ου αιώνα π.Χ. και την αρχή του 2ου αιώνα π.Χ. Είναι ο πρώτος γνωστός επιστήμονας που απόδειξε την εστιακή ιδιότητα του παραβολικού κατόπτρου. Χρησιμοποίησε τη γεωμετρική καμπύλη αποκαλούμενη κισσοειδές του Διοκλή για να λύσει το πρόβλημα της Δήλου, όπως αναφέρει ο Πρόκλος στα σχόλιά του περί του Ευκλείδη και αποδόθηκε στον Διοκλή από τον Γεμίνο.
Αποσπάσματα μιας εργασίας του Διοκλή περί εστίασης των κατόπτρων διασώθηκαν στα σχόλια του Ευτόκιου γύρω από το σύγγραμμα του Αρχιμήδη «Περί Σφαίρας και κύλινδρου» Η εστίαση των κατόπτρων είχε μεγάλη επιρροή στους Άραβες μαθηματικούς, ιδιαίτερα στον Αλαζηνό. Η πραγματεία περιέχει δέκα έξι θεωρήματα που αποδεικνύονται με κωνικές τομές. Ένα από τα αποσπάσματα περιέχει τα θεωρήματα επτά και οκτώ, τα οποία δίνουν λύση στο πρόβλημα της τομής μιας σφαίρας και ένα επίπεδο έτσι ώστε οι προκύπτοντες δύο όγκοι να είναι σε μια δεδομένη αναλογία.
Το θεώρημα δέκα δίνει λύση στο πρόβλημα του διπλασιασμού του κύβου και ισοδυναμεί με την επίλυση μιας ορισμένης κυβικής εξίσωσης. Ένα άλλο απόσπασμα περιέχει τις προτάσεις ένδεκα και δώδεκα, που χρησιμοποιούνται κισσοειδή για να λύσουν το πρόβλημα της εύρεσης δύο μεσαίων αναλογιών ανάμεσα σε δύο μεγέθη. Δεδομένου ότι αυτή η πραγματεία καλύπτει περισσότερα θέματα από την εστίαση των κατόπτρων, ίσως το έργο «Περί εστίασης των Κατόπτρων» να είναι επακόλουθο τριών πιο σύντομων εργασιών του Διοκλή
Κισσοειδές του Διοκλή
Το Κισσοειδές του Διοκλή είναι μία συγκεκριμένη καμπύλη της γεωμετρίας, της οποίας η μελέτη αποδίδεται στον Διοκλή το 100 π.Χ.. Ο Διοκλής προσπαθούσε εκείνη την εποχή να λύσει το πρόβλημα της Δήλου, όπως αναφέρει ο Πρόκλος στα σχόλιά του περί του Ευκλείδη. Το όνομα της καμπύλης προέρχεται από το σχήμα της που μοιάζει με φύλλο κισσού.
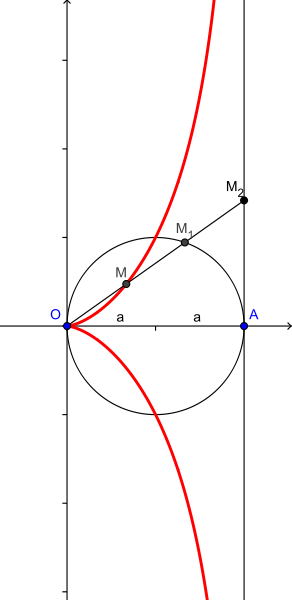
Ιδιότητες του κισσοειδούς
Τα σημεία της καμπύλης έχουν την εξής ιδιότητα:
Έχουμε έναν κύκλο με ακτίνα a, ένα σημείο S του κύκλου και μια εφαπτομένη που εφάπτεται στο σημείο διαμετρικά του σημείου S. Για κάθε σημείο P του κισσοειδούς, τα κοινά σημεία της ευθείας SP και του κύκλου τα ονομάζουμε K και τα κοινά σημεία της ευθείας SP με την εφαπτομένη τα ονομάζουμε A.

Εξίσωση του κισσοειδούς
Η καμπύλη εκφράζεται με τις εξής εξισώσεις:
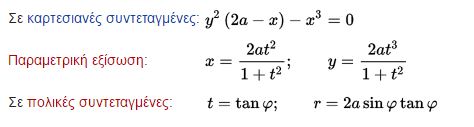
Διπλασιασμός του κύβου
Ο Διπλασιασμός του κύβου (επίσης γνωστός ως πρόβλημα της Δήλου - Δήλιον πρόβλημα) είναι ένα από τα τρία γνωστά προβλήματα της αρχαιότητας που δεν είναι δυνατόν να λυθούν μόνο με κανόνα και διαβήτη. Ήταν γνωστό στους μαθηματικούς της αρχαιότητας στην Αίγυπτο, την Ελλάδα και την Ινδία.
Το πρόβλημα συνίσταται στην κατασκευή ενός κύβου με διπλάσιο όγκο από ένα γνωστό κύβο πλευράς α. Ο απλός διπλασιασμός του μήκους της ακμής του κύβου οδηγεί σε οχταπλασιασμό του όγκου.
Ο μύθος
Αρκετοί μύθοι υπάρχουν για το λεγόμενο Δήλιο πρόβλημα. Ο Ερατοσθένης ο Κυρηναίος σύγχρονος του Αρχιμήδη σε επιστολή του προς τον Έλληνα Βασιλιά της Αιγύπτου Πτολεμαίο αναφέρει ότι σύμφωνα με πληροφορία αρχαίου τραγωδού ο Μίνωας είχε παραγγείλει να κατασκευαστεί τάφος για τον γιο του Γλαύκο σχήματος κυβικού. Όταν κατασκευάστηκε ο Μίνωας τον θεώρησε μικρό και διέταξε να τον διπλασιάσουν.
Ο Θέων ο Σμυρναίος σε ένα διάλογο του με τίτλο Πλατωνικός, του οποίου διασώζονται αποσπάσματα, αναφέρει ότι οι κάτοικοι της Δήλου αρρώστησαν και ζήτησαν από το Μαντείο των Δελφών να τους πει τι να κάνουν για να γλυτώσουν. Η Πυθία τους απάντησε ότι πρέπει να διπλασιάσουν σε όγκο τον ναό του Απόλλωνα που είχε σχήμα κύβου διατηρώντας παράλληλα το κυβικό σχήμα.
Οι Δήλιοι αρχικά πίστεψαν ότι το πρόβλημα ήταν απλό και λυνόταν με διπλασιασμό των πλευρών. Όταν ανακάλυψαν ότι αυτό δεν διπλασιάζει τον όγκο αλλά τον οχταπλασιάζει έστειλαν πρέσβεις στην Ακαδημία Πλάτωνος και ζήτησαν λύση του προβλήματος. Ο Πλάτωνας μάλιστα τους απάντησε ότι ο θεός έδωσε αυτόν τον χρησμό στους Δήλιους, όχι επειδή είχε ανάγκη ενός διπλάσιου βωμού, αλλά για να κατακρίνει και να επιπλήξει τους Έλληνες; επειδή αμελούν τα μαθηματικά και περιφρονούν τη γεωμετρία.
Το άλυτο του προβλήματος
Την εποχή που παρουσιάζεται το πρόβλημα κάθε μαθηματική μέθοδος που δεν χρησιμοποιεί αποκλειστικά κανόνα και διαβήτη θεωρείται ασέβεια. Οι αρχαίοι μαθηματικοί πιθανότατα γνώριζαν ότι ήταν αδύνατη η λύση μόνο με κανόνα και διαβήτη αλλά δεν έχει διασωθεί καμία απόδειξη.
Πιο κοντά στη λύση βρέθηκε ο Ιπποκράτης ο Χίος ο οποίος απέδειξε το 460 ή 430 π.Χ. ότι το πρόβλημα ανάγεται στην εύρεση δύο μέσων αναλόγων όταν δοθούν δύο ευθύγραμμα τμήματα το ένα διπλάσιο του άλλου. Από αυτό συνάγεται ότι για να λυθεί το πρόβλημα πρέπει να κατασκευαστεί ακμή ίση με 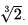 .
.
Με τα σύγχρονα μαθηματικά αποδείχθηκε ότι το πρόβλημα δεν είναι δυνατόν να λυθεί μόνο με κανόνα και διαβήτη και δόθηκε τέλος στην αναζήτηση λύσης αυτής της μορφής.
Η «λύση»
Αρκετοί αρχαίοι και νεώτεροι ασχολήθηκαν με το πρόβλημα όπως ο Αρχύτας ο Ταραντίνος, ο Εύδοξος ο Κνίδιος, ο Μέναιχμος, ο Νικομήδης, ο Απολλώνιος ο Περγαίος, ο Διοκλής, ο Ήρων ο Αλεξανδρεύς, ο Πάππος ο Αλεξανδρεύς, ο Καρτέσιος και άλλοι. Όλοι όμως έδιναν λύση που χρησιμοποιούσε και άλλες μεθόδους πλην της κλασσικής.
Ο Ευτόκιος ο Ασκαλωνίτης δίνει στα έργα του πληροφορίες για 12 λύσεις του Δήλιου προβλήματος. Σήμερα σημαντικότερη θεωρείται η λύση του Αρχύτα καθώς χρησιμοποιεί τρία στερεά: κύλινδρο, κώνο, και σφαίρα.
Πιο περίπλοκες μέθοδοι περιλαμβάνουν την Κισσοειδή του Διοκλή, την Κογχοειδή του Νικομήδη, ή τη γραμμή του Φίλωνα του Βυζαντινού.
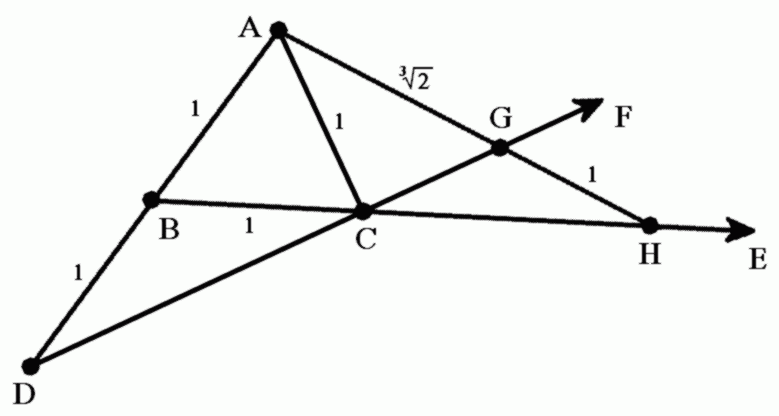
Κατασκευή
Υπάρχουν πολλοί τρόποι να κατασκευάσουμε 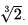 , αλλά χρειαζόμαστε βοηθητικά εργαλεία πέρα του διαβήτη και του χάρακα. Παραδείγματος χάριν:
, αλλά χρειαζόμαστε βοηθητικά εργαλεία πέρα του διαβήτη και του χάρακα. Παραδείγματος χάριν:

Τώρα πάρτε τον χάρακα και τοποθετήστε τον έτσι ώστε να αγγίζει το σημείο Α και να τέμνει την ημιευθεία 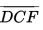 στο σημείο G και την ημιευθεία
στο σημείο G και την ημιευθεία 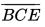 στο σημείο H, έτσι ώστε η απόσταση GH να είναι ακριβώς 1 μονάδα μήκους.
στο σημείο H, έτσι ώστε η απόσταση GH να είναι ακριβώς 1 μονάδα μήκους.
Το ευθύγραμμο τμήμα AG θα έχει το ζητούμενο μήκος 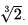 .
.
Βιβλιογραφια - Πηγες
[1] "School of Mathematics and Statistics University of St Andrews, Scotland " by J J O'Connor and E F Robertson
[2] "Wikipedia"
Αναφορές για το Διοκλή:
1. K H Dannenfeldt, G J Toomer, Biography in Dictionary of Scientific Biography (New York 1970-1990).
2. Biography in Encyclopaedia Britannica.
Βιβλία:
3. T L Heath, A History of Greek Mathematics (2 Vols.) (Oxford, 1921).
4. G J Toomer, Diocles On Burning Mirrors, Sources in the History of Mathematics and the Physical Sciences 1 (New York, 1976).
Άρθρα:
6. J P Hogendijk, Diocles and the geometry of curved surfaces, Centaurus 28 (3-4) (1985), 169-184.
7. O Neugebauer, Note on Diocles' 'burning mirror', in From ancient omens to statistical mechanics, Acta Hist. Sci. Nat. Med. 39 (Copenhagen, 1987), 37-42.