Ancient Greece Reloaded

ANCIENT GREECE RELOADED

ΜΠΕΣ ΣΤΟΝ ΚΟΣΜΟ ΤΩΝ ΜΥΘΩΝ ΚΑΙ ΤΩΝ ΘΡΥΛΩΝ

Ερατοσθενης ο Κυρηναιος

ΠΗΓΑΙΝΕ ΑΠΕΥΘΕΙΑΣ ΣΤΙΣ ΑΚΟΛΟΥΘΕΣ ΕΝΟΤΗΤΕΣ:

ΒΙΟΓΡΑΦΙΑ

TΟ ΚΟΣΚΙΝΟ ΤΟΥ ΕΡΑΤΟΣΘΕΝΗ

Ο ΕΡΑΤΟΣΘΕΝΗΣ ΚΑΙ Η ΑΚΤΙΝΑ ΤΗΣ ΓΗΣ

O CARL SAGAN ΕΞΗΓΕΙ ΤΗ ΜΕΤΡΗΣΗ ΤΟΥ ΕΡΑΤΟΣΘΕΝΗ (Με Ελληνικούς Υπότιτλους)

Ο Ερατοσθένης (Κυρήνη 276 π.Χ. – Αλεξάνδρεια 194 π.Χ.) ήταν αρχαίος Έλληνας μαθηματικός, γεωγράφος, αστρονόμος, γεωδαίτης, ιστορικός και φιλόλογος. Θεωρείται ο πρώτος που υπολόγισε το μέγεθος της Γης και κατασκεύασε ένα σύστημα συντεταγμένων με παράλληλους και μεσημβρινούς. Ακόμα κατασκεύασε ένα χάρτη του κόσμου όπως τον θεωρούσε.

Αν και ο Ερατοσθένης γεννήθηκε στην Κυρήνη (στη σημερινή Λιβύη), έζησε, εργάστηκε και πέθανε στην Αλεξάνδρεια, πρωτεύουσα της πτολεμαϊκής Αιγύπτου.

Σπούδασε στην Αλεξάνδρεια και ισχυριζόταν ότι επίσης σπούδασε για κάποια χρόνια στην Αθήνα. Το 236 π.Χ. ορίστηκε από τον Πτολεμαίο τον Γ΄ τον Ευεργέτη βιβλιοθηκάριος της Βιβλιοθήκης της Αλεξάνδρειας, διαδεχόμενος τον Ζηνόδοτο. Από το 234 π.Χ και επί περίπου 40 χρόνια διετέλεσε υπεύθυνος της περίφημης αυτής βιβλιοθήκης και δίδαξε στο Μουσείο της.

Δεν νυμφεύθηκε ποτέ. Το 194 π.Χ. τυφλώθηκε και ένα χρόνο αργότερα σταμάτησε να τρώει και πέθανε. Δεν μπόρεσε να αντέξει τη στέρηση της ανθρώπινης γνώσης που του επέβαλε η τύφλωση.

ΤΟ ΕΡΓΟ ΤΟΥ

Έκανε αρκετές σημαντικές συνεισφορές στα μαθηματικά και ήταν φίλος του σπουδαίου μαθηματικού Αρχιμήδη. Γύρω στο 225 π.Χ. εφηύρε τον σφαιρικό αστρολάβο, που τον χρησιμοποιούσαν ευρέως μέχρι τον 18ο αιώνα.

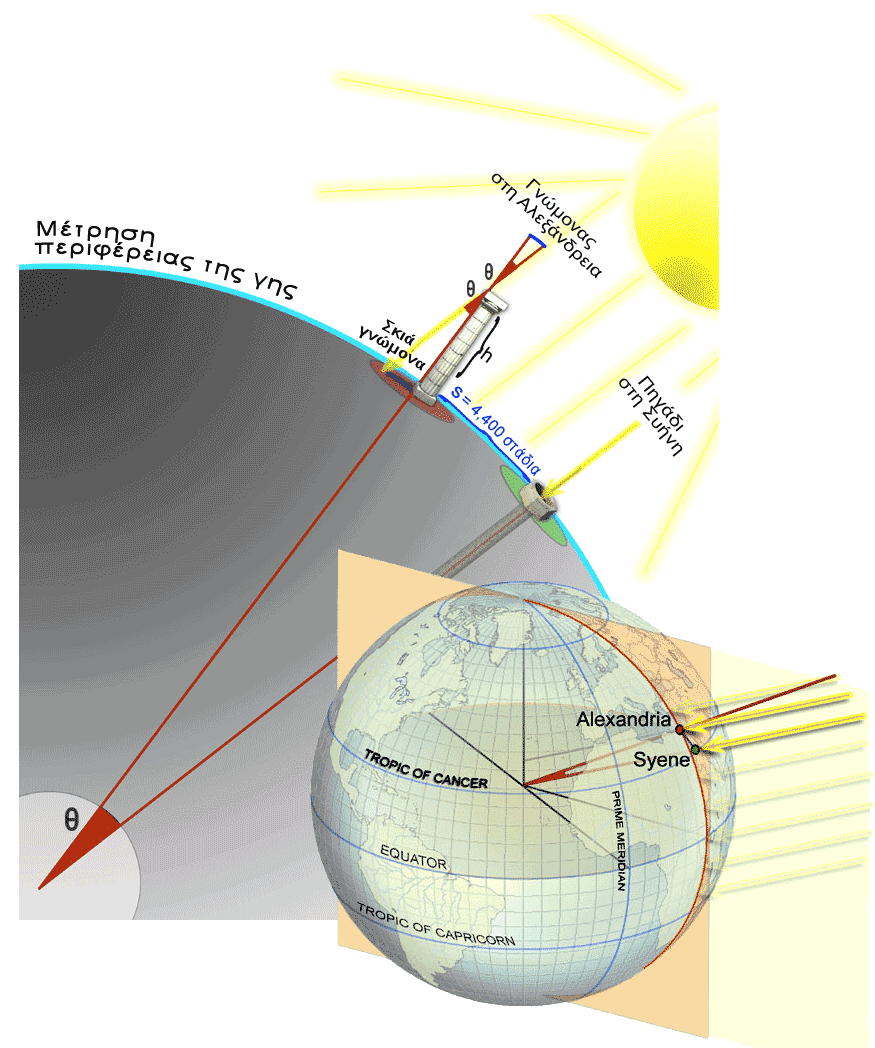
Αναφέρεται από τον Κλεομήδη στο Περί της κυκλικής του κινήσεως των ουρανίων σωμάτων ότι γύρω στο 240 π.Χ. υπολόγισε την περιφέρεια της Γης χρησιμοποιώντας το ύψος του Ηλίου κατά το θερινό ηλιοστάσιο σε δύο διαφορετικά γεωγραφικά σημεία, που όμως βρίσκονταν στον ίδιο (περίπου) μεσημβρινό: κοντά στην Αλεξάνδρεια και στη νήσο Ελεφαντίνη -όπου ο Ήλιος ήταν στο ζενίθ του ουρανού- κοντά στη Συήνη (σημερινό Ασουάν, Αίγυπτος).

Ο Ερατοσθένης υπολόγισε την περιφέρεια της Γης σε 252.000 στάδια. Δεν ξέρουμε όμως την ακρίβεια της μέτρησης, καθώς δεν ξέρουμε ποιο είδος σταδίου χρησιμοποίησε. Αν χρησιμοποίησε το αττικό στάδιο (184,98 μέτρα), τότε υπολόγισε την περιφέρεια σε 46.615 χιλιόμετρα. Αν χρησιμοποίησε το οδοιπορικό στάδιο (157,50 μέτρα), τότε την υπολόγισε σε 39.690 χιλιόμετρα, που είναι αρκετά καλός υπολογισμός, με δεδομένο ότι σήμερα υπολογίζεται σε 40.007,86 χιλιόμετρα, ενώ στη Γαλλική Επανάσταση είχε οριστεί να είναι 40.000 χιλιόμετρα.

Ήταν ο πρώτος που υποστήριξε ότι η Γη είναι μια σφαίρα που βρίσκεται στο κέντρο του Σύμπαντος, το οποίο περιστρέφεται με συχνότητα εικοσιτεσσάρων ωρών. Επινόησε επίσης το σύστημα των γεωγραφικών παραλλήλων. Διατύπωσε την υπόθεση ότι είναι δυνατό να ταξιδέψουμε κατά μήκος μιας γεωγραφικής παράλληλου ξεκινώντας από την Ιβηρία και να φτάσουμε έως την Ινδία, διαπλέοντας τον Ατλαντικό Ωκεανό. Ο Στράβων, που διέσωσε και μας μετέφερε την θεωρία αυτή, προσέθεσε μάλιστα, ότι στο ταξίδι αυτό ίσως να συναντούσαμε νέα άγνωστα μέρη ξηράς.

Επίσης εφηύρε έναν τρόπο υπολογισμού των πρώτων αριθμών γνωστό ως κόσκινο του Ερατοσθένη.

Ο όρος Γεωγραφία αποδίδεται στον Ερατοσθένη.

ΕΡΓΑ

Από τα ποικίλα έργα του δεν σώθηκε κανένα εκτός από λίγους τίτλους, όπως:

"Χρονογραφίαι" (9 βιβλία): Χρονολογική ταξινόμηση ανθρώπων και γεγονότων.

"Γεωγραφικά" (3 βιβλία): Η Μαθηματική γεωγραφία και η ιστορία της.

"Περί της Αρχαίας κωμωδίας": Κριτική, ιστορία και χρονολόγηση.

"Καταστερισμοί": Μελέτη των αστερισμών.

"Περί Μεσοτήτων": Μελέτη της Αριθμητικής Γεωμετρικής και Αρμονικής αναλογίας.

Επιστήθιος φίλος του Αρχιμήδη διατηρούσε επαφή μαζί του και συμμετείχε στα γεωμετρικά ζητούμενα της εποχής του. Δυστυχώς όμως από το συνολικό μαθηματικό του έργο δεν σώθηκε τίποτα. Σώθηκε όμως η μνήμη δύο μαθηματικών του επιτυχιών.

Επινόησε και κατασκεύασε το περίφημο όργανο "Μεσολάβιον", με τη βοήθεια του οποίου έλυε το Δήλιο πρόβλημα (διπλασιασμό του κύβου), και ταυτόχρονα μπορούσε να παρεμβάλει ανάμεσα σε δύο δοσμένα ευθύγραμμα τμήματα δύο μέσες αναλόγους, σε συνεχή αναλογία.

Στα περίφημα "Γεωγραφικά" του παρουσίασε την πρώτη ακριβή μαθηματική μέτρηση της περιμέτρου της Γης, με την βοήθεια σκιοθηρικών γνωμόνων, και την βρήκε ίση με 250.000 στάδια (=39.400-41.000 km, έναντι της πραγματικής 40.000 km) (Κλεομήδης, Στράβων).

Πιστεύεται ότι ανακάλυψε ακόμα μία μέθοδο υπολογισμού της διάρκειας των μεγίστων ημερών στα διάφορα πλάτη, από το γεωγραφικό πλάτος τους, και ότι συγκρότησε πίνακα πλατών γνωστών τόπων.

Κατασκεύασε τον πρώτο παγκόσμιο μαθηματικό χάρτη της τότε οικουμένης, την οποία σχεδίασε πάνω σε ένα πλέγμα καθέτων ευθειών (μεσημβρινών και παραλλήλων κύκλων), αξιοποιώντας τις πληροφορίες των γεωγραφικών έργων της βιβλιοθήκης και των έργων των συνοδών του Μ. Αλεξάνδρου στην εκστρατεία της Ασίας.

TΟ ΚΟΣΚΙΝΟ ΤΟΥ ΕΡΑΤΟΣΘΕΝΗ

Στα μαθηματικά, το Κόσκινο του Ερατοσθένη είναι ένας απλός αλγόριθμος για την εύρεση όλων των πρώτων αριθμών μέχρι έναν συγκεκριμένο ακέραιο. Σαν αλγόριθμος είναι γρήγορος για μικρούς πρώτους (κάτω από 10 εκατομμύρια). Δημιουργήθηκε από τον Ερατοσθένη, μαθηματικό της Αρχαίας Ελλάδας. Αν και κανένα από τα μαθηματικά του έργα δεν έχει διασωθεί, το κόσκινο περιγράφεται και αποδίδεται στον Ερατοσθένη στην Εισαγωγή στην Αριθμητική του Νικόμαχου.

Πρώτος αριθμός

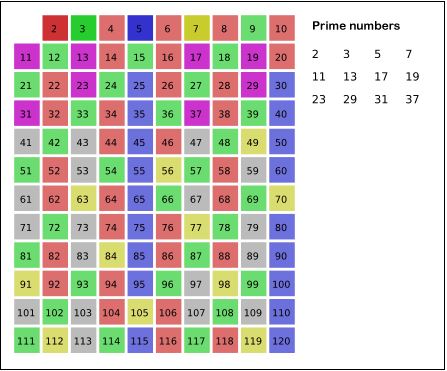
Στα μαθηματικά πρώτος αριθμός (ή απλά πρώτος) είναι ένας φυσικός αριθμός μεγαλύτερος της μονάδας με την ιδιότητα οι μόνοι φυσικοί διαιρέτες του να είναι η μονάδα και ο εαυτός του. Ένας φυσικός αριθμός μεγαλύτερος της μονάδας , ο οποίος δεν είναι πρώτος αριθμός ονομάζεται σύνθετος αριθμός. Για παράδειγμα, ο αριθμός 5 είναι πρώτος, επειδή μόνο οι αριθμοί 1 και 5 τον διαιρούν εξίσου, ενώ ο 6 είναι σύνθετος επειδή έχει διαιρέτες τους 2 και 3 εκτός των 1 και 6. Το μηδέν και το ένα δεν είναι πρώτοι αριθμοί. Το μηδέν συχνά δεν θεωρείται καν φυσικός αριθμός.

Η ακολουθία των 25 πρώτων αριθμών είναι η εξής:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, ...

Ο αριθμός 2 είναι ο μόνος άρτιος (ζυγός) πρώτος αριθμός. Όλοι οι άλλοι πρώτοι είναι περιττοί (μονοί).

Αλγόριθμος

Ένας πρώτος αριθμός είναι ένας φυσικός αριθμός που έχει ακριβώς δύο διαφορετικούς διαιρέτες: το 1 και τον εαυτό του.

Η εύρεση όλων των πρώτων αριθμών που είναι μικρότεροι ή ίσοι από έναν ακέραιο n, σύμφωνα με τη μέθοδο του Ερατοσθένη, γίνεται ως εξής:

Δημιουργούμε μια λίστα από διαδοχικούς ακέραιους από το 2 μέχρι το n: (2, 3, 4, ..., n).

Αρχικά, έστω ότι το p είναι ίσο με 2, τον 1ο πρώτο αριθμό.

Διαγράφουμε από τη λίστα όλα τα πολλαπλάσια του p που είναι μικρότερα ή ίσα με n. (2p, 3p, 4p, κτλ)

Βρίσκουμε τον 1ο αριθμό που απομένει στη λίστα μετά τον p (αυτός ο αριθμός είναι ο επόμενος πρώτος αριθμός) και αντικαθιστούμε το p με αυτόν τον αριθμό.

Επαναλαμβάνουμε τα βήματα 3 και 4 μέχρι το p2 να είναι μεγαλύτερο από n.

Όλοι οι αριθμοί που απομένουν στη λίστα είναι πρώτοι αριθμοί.

Παράδειγμα

Για να βρούμε όλους τους πρώτους αριθμούς που είναι μικρότεροι ή ίσοι από το 30, εργαζόμαστε ως εξής: Αρχικά δημιουργούμε μια λίστα από τους ακέραιους από το 2 έως το 30:

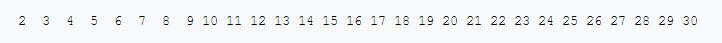
Διαγράφουμε τα πολλαπλάσια του 2 με αποτέλεσμα:

Ο 1ος αριθμός στη λίστα μετά το 2 είναι το 3 και διαγράφουμε τα πολλαπλάσια του 3 από τη λίστα με αποτέλεσμα:

Ο 1ος αριθμός στη λίστα μετά το 3 είναι το 5 και διαγράφουμε τα πολλαπλάσια του 5 από τη λίστα με αποτέλεσμα:

Ο 1ος αριθμός στη λίστα μετά το 5 είναι το 7 αλλά το τετράγωνο του 7 είναι 49 που είναι μεγαλύτερο από το 30, επομένως η διαδικασία τελείωσε. Η τελική λίστα αποτελείται από όλους τους πρώτους αριθμούς που είναι μικρότεροι ή ίσοι από 30.

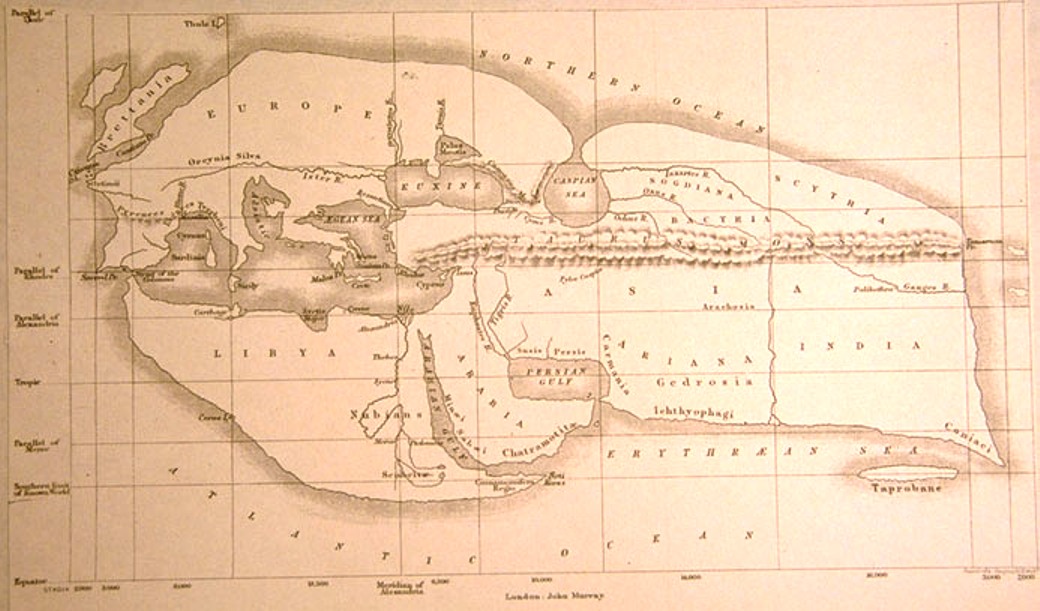
Ο Παγκόσμιος Χάρτης του Ερατοσθένη

Πήγαινε: στην Αρχή της Σελίδας

Ο Ερατοσθενης και η ακτινα της Γης

Οι αρχαίοι Ελληνες, αντίθετα με όσα πιστεύει ο μέσος πολίτης σήμερα, γνώριζαν από την εποχή του Αριστοτέλη ότι η Γη είναι σφαιρική και όχι επίπεδη. Ο Ερατοσθένης μάλιστα, με ένα πείραμα που έχει μείνει στην Ιστορία, μπόρεσε να μετρήσει την ακτίνα της Γης με ακρίβεια απρόσμενη για τα μέσα της εποχής εκείνης. Οι μεταγενέστεροι αστρονόμοι και γεωγράφοι όμως συντάχθηκαν με την άποψη του Πτολεμαίου ότι η Γη είναι 30% μικρότερη από όσο είχε μετρήσει ο Ερατοσθένης. Το λάθος αυτό παρέμεινε για 15 αιώνες και ήταν η αιτία να αποφασίσει ο Κολόμβος το ταξίδι για την Ινδία, το οποίο κατέληξε στην ανακάλυψη της Αμερικής.

Στον τροπικό του Καρκίνου

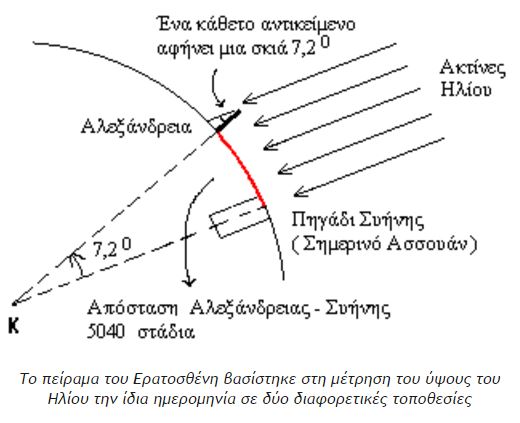
Το πείραμα του Ερατοσθένη βασίστηκε στη μέτρηση του ύψους του Ηλίου την ίδια ημερομηνία σε δύο διαφορετικές τοποθεσίες, καθώς και στην πεποίθηση του μεγάλου έλληνα μαθηματικού ότι ο Ηλιος είναι πολύ μακριά από τη Γη, τόσο ώστε οι ακτίνες του να φθάνουν στον πλανήτη μας σχεδόν παράλληλα. Από διηγήσεις ταξιδιωτών ο Ερατοσθένης έμαθε ότι στις 21 Ιουνίου, την ημέρα του θερινού ηλιοστασίου, ο Ηλιος καθρεφτίζεται στην επιφάνεια του νερού των πηγαδιών της πόλης Συήνης, αυτής που σήμερα οι Αιγύπτιοι ονομάζουν Ασουάν.

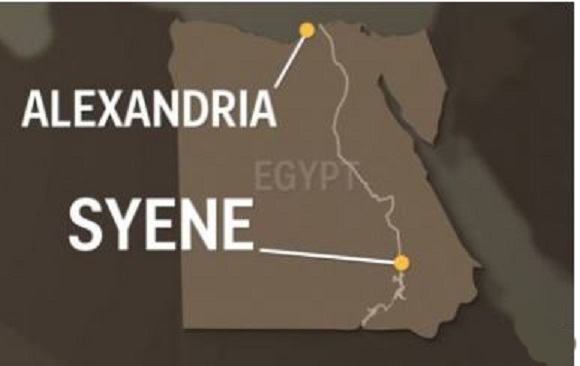
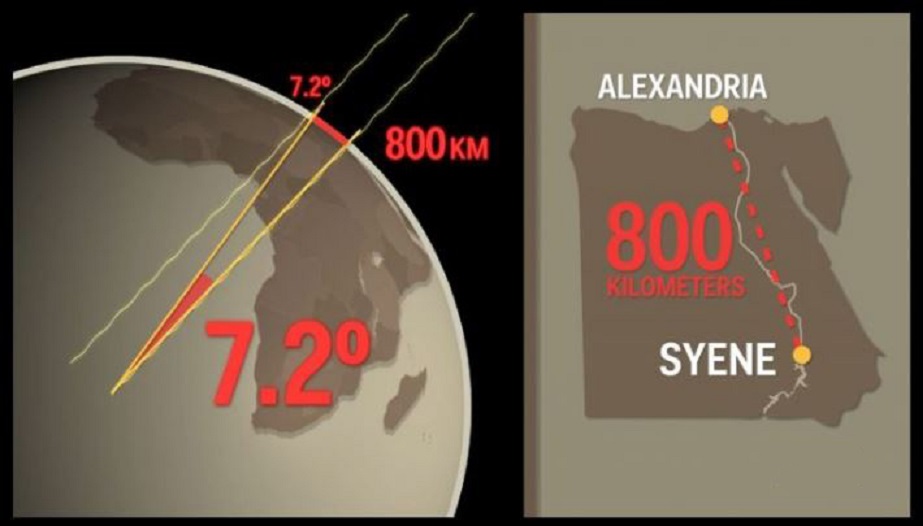
Από την πληροφορία αυτή ο Ερατοσθένης συμπέρανε ότι η Συήνη βρίσκεται πάνω στον τροπικό του Καρκίνου, δηλαδή στον παράλληλο κύκλο με γεωγραφικό πλάτος 23,5 μοίρες. Το χαρακτηριστικό των τόπων που βρίσκονται στον τροπικό του Καρκίνου είναι ότι το μεσημέρι της 21ης Ιουνίου ο Ηλιος βρίσκεται στο ζενίθ, δηλαδή ακριβώς κατακόρυφα προς τα πάνω. Ετσι οι ακτίνες του διαδίδονται κατά μήκος των κατακόρυφων τοιχωμάτων των πηγαδιών, ανακλώνται στην επιφάνεια του νερού και επιστρέφουν προς την επιφάνεια, κάνοντας ορατό το είδωλό του σε έναν παρατηρητή που κοιτάζει από το στόμιο του πηγαδιού.

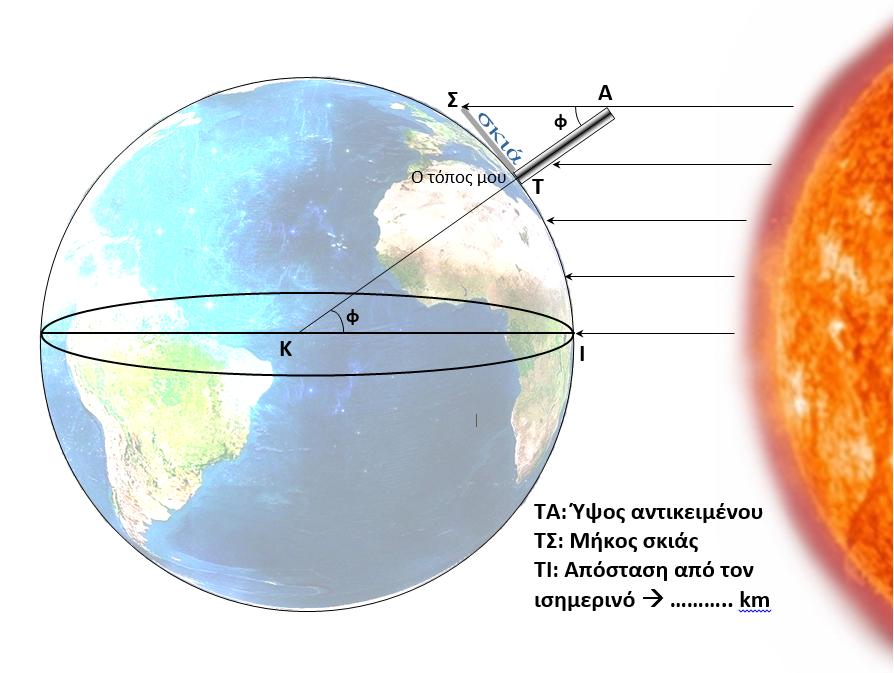
Το μεσημέρι της ημέρας του θερινού ηλιοστασίου ο Ερατοσθένης μέτρησε το ύψος του Ηλίου στην πόλη στην οποία κατοικούσε, την Αλεξάνδρεια της Αιγύπτου. Η μέτρηση έγινε με τη βοήθεια ενός οβελίσκου, ο οποίος είναι το αρχαιότερο αστρονομικό όργανο στην ιστορία της επιστήμης. Το μήκος της σκιάς που ρίχνει ο οβελίσκος, διαιρεμένο με το ύψος του οβελίσκου, μας δίνει, όπως μάθαμε στο σχολείο, την εφαπτομένη της γωνίας του ύψους του Ηλίου. Η γωνία αυτή, η οποία από τη μέτρηση του Ερατοσθένη προέκυψε 7,2 μοίρες, είναι ίση (ως «εντός-εκτός και επί τα αυτά», όπως θυμούνται οι παλαιότεροι) με την επίκεντρη γωνία που σχηματίζουν δύο ακτίνες της Γης με άκρα τη Συήνη και την Αλεξάνδρεια, υπό την προϋπόθεση ότι οι δύο πόλεις έχουν το ίδιο γεωγραφικό μήκος, βρίσκονται δηλαδή στον ίδιο μεσημβρινό.

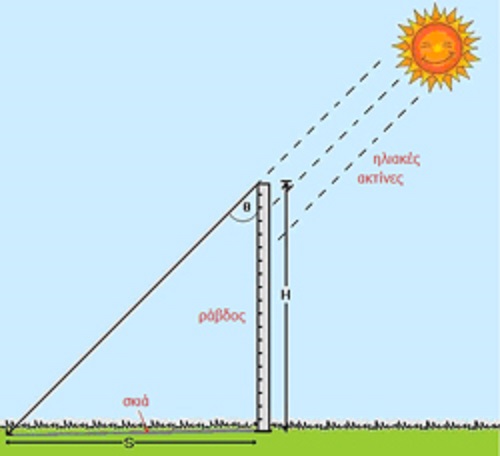
Επειδή από τη γεωμετρία γνωρίζουμε ότι η απόσταση των δύο πόλεων, η ακτίνα της Γης και η γωνία που μέτρησε ο Ερατοσθένης συνδέονται με τη σχέση απόσταση/ακτίνα = 6,28x(7,2/360), η ακτίνα της Γης βρίσκεται αμέσως αν γνωρίζουμε την απόσταση των δύο πόλεων. Την εποχή του Ερατοσθένη, περί το 250 π.Χ., δεν υπήρχε ακριβής μέθοδος μέτρησης τόσο μεγάλων αποστάσεων. Σύμφωνα με την παράδοση, ο Ερατοσθένης ανέθεσε σε επαγγελματίες βαδιστές να την υπολογίσουν, και το αποτέλεσμά τους το συνέκρινε με τις εκτιμήσεις αρχηγών καραβανιών. Το τελικό του αποτέλεσμα ήταν ότι η απόσταση Αλεξάνδρειας- Συήνης ισούται με 5.000 στάδια, οπότε η ακτίνα της Γης προκύπτει ίση με 252.000 στάδια.

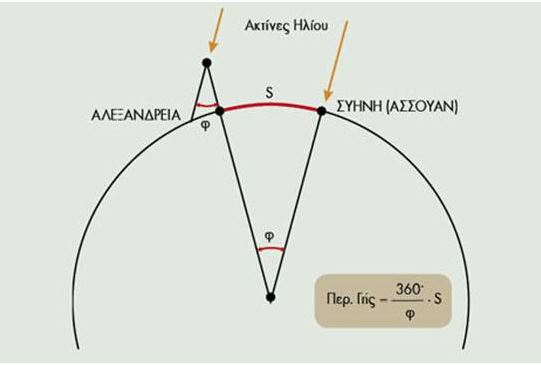
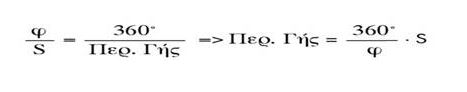
Για να μπορέσουμε να εκτιμήσουμε την ακρίβεια της μέτρησης του Ερατοσθένη, θα έπρεπε να γνωρίζουμε πόσο είναι το μήκος ενός σταδίου σε μέτρα, καθώς και κατά πόσο αληθεύουν οι δύο υποθέσεις του Ερατοσθένη, δηλαδή ότι η Συήνη έχει γεωγραφικό πλάτος 23,5 μοίρες και ότι Συήνη και Αλεξάνδρεια βρίσκονται στον ίδιο μεσημβρινό. Μια ματιά σε έναν σύγχρονο χάρτη δείχνει ότι και οι δύο υποθέσεις ήταν λανθασμένες, αλλά το λάθος δεν ήταν μεγάλο: το γεωγραφικό πλάτος της Συήνης είναι 24,1 μοίρες, ενώ τα γεωγραφικά μήκη των δύο πόλεων διαφέρουν μόνο κατά μία μοίρα. Επομένως η βασική πηγή σφάλματος είναι το μήκος ενός σταδίου σε μέτρα. Θα έλεγε κανείς ότι έχουν διασωθεί πολλά αρχαία στάδια, οπότε δεν έχουμε παρά να μετρήσουμε πόσο μήκος έχει ένα από αυτά.

Δυστυχώς τα στάδια δεν είχαν το ίδιο μήκος σε όλες τις περιοχές της αρχαίας Ελλάδας. Αν υποθέσουμε ότι ο Ερατοσθένης εννοούσε αττικά στάδια των 185 μέτρων, τότε το αποτέλεσμά του δίνει για την ακτίνα της Γης 7.400 χιλιόμετρα, τιμή 16% μεγαλύτερη από την πραγματική. Αν όμως εννοούσε αιγυπτιακά στάδια, πράγμα που είναι και το πιθανότερο, τότε κατά τον Ερατοσθένη η ακτίνα της Γης είναι 6.316 χιλιόμετρα, μόλις 1% μικρότερη από την πραγματική, που σήμερα γνωρίζουμε ότι είναι 6.366 χιλιόμετρα!

Πώς ξεγελάστηκε ο Κολόμβος

Το πείραμα του Ερατοσθένη είχε δημιουργήσει μεγάλη εντύπωση στην εποχή του, και αρκετοί μεταγενέστεροι φυσικοί φιλόσοφοι, όπως ονομάζονταν οι επιστήμονες εκείνη την εποχή, θέλησαν να το επαναλάβουν. Ο πρώτος που γνωρίζουμε, χρονολογικά, ήταν ο Ελληνας Ποσειδώνιος ο Ρόδιος, ο οποίος γύρω στο 100 π.Χ. υπολόγισε την ακτίνα της Γης με διαφορετική μέθοδο από αυτήν του Ερατοσθένη. Υπέθεσε ότι η Αλεξάνδρεια και η Ρόδος είναι στον ίδιο μεσημβρινό και υπολόγισε ότι η επίκεντρη γωνία που σχηματίζουν οι δύο πόλεις είναι 7,5 μοίρες, παρατηρώντας όχι τον Ηλιο αλλά το ύψος του αστέρα Κάνωπου, όπως φαίνεται από τις δύο πόλεις.

Υποθέτοντας ότι η απόσταση των δύο πόλεων είναι 5.000 στάδια, κατέληξε σε ένα αποτέλεσμα πρακτικά ίδιο με αυτό του Ερατοσθένη. Μεταγενέστερα όμως αναθεώρησε την εκτίμησή του για την απόσταση Ρόδου- Αλεξάνδρειας σε 3.750 στάδια, οπότε η ακτίνα της Γης προέκυψε ίση με 4.500 χιλιόμετρα, δηλαδή 30% μικρότερη από την πραγματική. Με την τιμή αυτή συμφώνησε στη συνέχεια ο ρωμαίος ναύαρχος και φυσικός φιλόσοφος Πλίνιος, ενώ την καθιέρωσε οριστικά ο έλληνας αστρονόμος Πτολεμαίος αναφέροντάς τη στο βιβλίο του Γεωγραφία.

Τα βιβλία του Πτολεμαίου έχαιραν μεγάλης εκτίμησης μεταξύ των επιστημόνων ως την Αναγέννηση, και αυτό το γεγονός ήταν η αιτία να επικρατήσει τελικά η λανθασμένη τιμή του Ποσειδώνιου για την ακτίνα της Γης. Σε υδρόγειες σφαίρες της εποχής, κατασκευασμένης με βάση αυτήν τη λανθασμένη τιμή, βλέπει κανείς τοποθετημένες την Ευρώπη, την Ασία και την Αφρική να καλύπτουν όλη την επιφάνεια της Γης, χωρίς να υπάρχει διαθέσιμος χώρος για άλλη ήπειρο. Ο Κολόμβος, με βάση παρόμοιους χάρτες, κατέληξε στο συμπέρασμα ότι η Ινδία απείχε από τα Κανάρια Νησιά μόλις 6.300 χιλιόμετρα δυτικά (αντί για τη σωστή 28.000 χιλιόμετρα), οπότε θα μπορούσε να φθάσει σχετικά σύντομα στις Ινδίες ταξιδεύοντας προς δυσμάς.

Επομένως θα μπορούσε κανείς να πει ότι το λάθος του Ποσειδώνιου έπαιξε καθοριστικό ρόλο για την ανακάλυψη της Αμερικής από τον Κολόμβο, αφού είναι σχεδόν βέβαιο ότι αν γνώριζε τις πραγματικές διαστάσεις της Γης δεν θα τολμούσε ποτέ να ξεκινήσει για ένα ταξίδι 28.000 χιλιομέτρων με τα πλοία της εποχής.