ΙΠΠΟΚΡΑΤΗΣ Ο ΧΙΟΣ
Ο Ιπποκράτης ο Χίος (περ. 470 – 400 π.Χ) ήταν αρχαίος Έλληνας μαθηματικός, που διακρίθηκε στη γεωμετρία και έζησε τον 5ο αιώνα π.Χ, ήταν δηλαδή σχεδόν σύγχρονος του Σωκράτη. Θεωρείται ο κύριος εκπρόσωπος της Σχολής της Χίου.
Βιογραφικά Στοιχεία
Ο Ιπποκράτης γεννήθηκε στο νησί Χίος, όπου, καθώς μας πληροφορεί ο Αριστοτέλης στα «Ηθικά Ευδήμεια», ήταν αρχικώς έμπορος ή εφοπλιστής. Απώλεσε την περιουσία του στο Βυζάντιο εξαιτίας απάτης των τελωνειακών υπαλλήλων (ή ληστεύτηκε από Αθηναίους πειρατές) και πήγε στην Αθήνα για δικαστική διεκδίκηση αποζημιώσεως. Εκεί όμως εξελίχθηκε σε κορυφαίο μαθηματικό. Ο Πλούταρχος στο έργο του Βίοι παράλληλοι (και συγκεκριμένα στον «Βίο του Σόλωνος») αναφέρει τον Ιπποκράτη τον Χίο ως «μαθηματικό και έμπορο». Για την ιδιότητα του σπουδαίου μαθηματικού γράφει και πάλι ο Αριστοτέλης στα Μετεωρολογικά του, όπου τον κατατάσσει ως ισάξιο των Αναξαγόρα, Δημοκρίτου και των κορυφαίων Πυθαγορείων φιλοσόφων. Αλλά και ο Πρόκλος χαρακτηρίζει τον Ιπποκράτη τον Χίο σπουδαίο μαθηματικό και τον τοποθετεί στον κατάλογο των μαθηματικών μετά τον Οινοπίδη.
Στη Χίο, ο Ιπποκράτης ίσως να υπήρξε προσωπικά μαθητής του μαθηματικού Οινοπίδη. Στην Αθήνα όμως άνοιξε ο ίδιος σχολή, στην οποία δίδασκε Γεωμετρία. Στο μαθηματικό έργο του Ιπποκράτους πιθανώς υπάρχει και κάποια πυθαγόρεια επίδραση, καθώς η Χίος γειτονεύει με τη Σάμο, την πατρίδα του Πυθαγόρα και κέντρο της πυθαγόρειας σκέψεως: ο Ιπποκράτης έχει χαρακτηρισθεί ως «παρα-πυθαγόρειος», ένας φιλοσοφικός «συνταξιδιώτης» των πυθαγόρειων στον κόσμο των ιδεών. Η «Εις άτοπον απαγωγή» (Reductio ad absurdum) ως μέθοδος μαθηματικών αποδείξεων έχει αποδοθεί σε αυτόν. Στην Αθήνα ο Ιπποκράτης παρέμεινε μέχρι το τέλος της ζωής του και πέθανε εκεί.
Μαθηματικά
Το βασικό έργο ζωής του Ιπποκράτη του Χίου είναι ότι υπήρξε ο πρώτος στην Ιστορία της Επιστήμης που συνέγραψε μια συστηματικά οργανωμένη πραγματεία γεωμετρίας, τα «Στοιχεία» (δηλαδή τα θεμελιώδη θεωρήματα ή οι «δομικοί λίθοι» της μαθηματικής θεωρίας). Αυτό ήταν ένα πολύ σημαντικό βήμα προόδου επειδή από τότε και μετά οι μαθηματικοί σε όλο τον αρχαίο κόσμο θα μπορούσαν να «χτίζουν» τις ιδέες τους πάνω σε ένα κοινό για όλους πλαίσιο βασικών εννοιών, μεθόδων και θεωρημάτων, γεγονός που συνετέλεσε στην πρόοδο των μαθηματικών.
Μόνο ένα, αλλά διάσημο, απόσπασμα των «Στοιχείων» του Ιπποκράτη (που δεν πρέπει να συγχέονται με τα «Στοιχεία» του Ευκλείδη) διασώθηκε μέχρι τις ημέρες μας, ενσωματωμένο σε έργο του Σιμπλίκιου. Σε αυτό το απόσπασμα υπολογίζεται το εμβαδό των σχημάτων που είναι σήμερα γνωστά διεθνώς ως Μηνίσκοι του Ιπποκράτους (ημισεληνοειδή τμήματα που περικλείονται από δύο κυκλικά τόξα). Αυτό εντασσόταν τότε σε ένα ερευνητικό πρόγραμμα για την επίτευξη του «τετραγωνισμού του κύκλου». Προφανώς η στρατηγική ήταν να υποδιαιρεθεί ένας κυκλικός δίσκος σε ημισεληνοειδή μέρη: αν ήταν δυνατός ο υπολογισμός του εμβαδού του καθενός από αυτά τα μέρη, τότε το εμβαδό ολόκληρου του δίσκου θα μπορούσε να εξαχθεί. Μόλις το 1882 μ.Χ. αποδείχθηκε ότι αυτή η προσέγγιση δεν είχε ελπίδα επιτυχίας, επειδή ο αριθμός π είναι ένας υπερβατικός αριθμός, οπότε δεν είναι κατασκευάσιμος με κανόνα και διαβήτη.
Στον αιώνα μετά τον Ιπποκράτη, τουλάχιστον 4 άλλοι μαθηματικοί συνέγραψαν τα δικά τους «Στοιχεία», βελτιώνοντας σταθερά την ορολογία και τη λογική τους δομή. Με αυτό τον τρόπο, η πρωτοπόρα δουλειά του Ιπποκράτη έθεσε τα θεμέλια και για τα «Στοιχεία» του Ευκλείδη (περ. 325 π.Χ.), που παρέμεινε το πρότυπο εγχειρίδιο γεωμετρίας μέχρι σχεδόν την εποχή μας.
Δύο άλλες συνεισφορές του Ιπποκράτη αξίζει να σημειωθούν. Ανακάλυψε μια (άγνωστη σε εμάς) μέθοδο χειρισμού του προβλήματος του «διπλασιασμού του κύβου», δηλαδή του προβλήματος της κατασκευής της κυβικής ρίζας του 2. Αυτό ήταν το άλλο μεγάλο μαθηματικό πρόβλημα της αρχαιότητας. Ο Ιπποκράτης επίσης επινόησε τη μέθοδο της μετατροπής ειδικότερων μαθηματικών προβλημάτων σε ένα γενικότερο πρόβλημα που είναι ευκολότερο να επιλυθεί. Η λύση στο γενικότερο πρόβλημα δίνει τότε αυτομάτως τη λύση του αρχικού προβλήματος.
Αστρονομία
Στο πεδίο της Αστρονομίας ο Ιπποκράτης προσπάθησε να εξηγήσει την εμφάνιση των κομητών και του Γαλαξία. Οι ιδέες του δεν έχουν μεταφερθεί ως την εποχή μας πολύ καθαρά, αλλά πιθανώς υπέθετε ότι αμφότερα ήταν οπτικές απάτες, το αποτέλεσμα της διαθλάσεως του ηλιακού φωτός από την υγρασία που ανέδινε ένας υποθετικός πλανήτης κοντά στον Ήλιο (στην πρώτη περίπτωση) και οι αστέρες (στην περίπτωση του Γαλαξία).
Η συμβολή του στην γεωμετρία ήταν η παρακάτω:
Eγραψε τα πρώτα "Στοιχεία" γεωμετρίας, στα οποία μάλλον τακτοποιούσε κάποια θεωρητικά ζητήματα (Πρόκλος). Είναι πιθανό να κατείχε την πρώτη γεωμετρία του Αναξίμανδρου.
Ασχολήθηκε με το πρόβλημα του Διπλασιασμού του Κύβου (κατασκευή του x από την x3=2α3, με α δοσμένο τμήμα), το οποίο τότε περίπου είχε τεθεί, και το ανήγαγε σε πρόβλημα αναλογιών (με τη μορφή της συνεχούς αναλογίας 2αy=yx=xα.
Ασχολήθηκε με το πρόβλημα του τετραγωνισμού του κύκλου, από την μελέτη του οποίου οδηγήθηκε στον τετραγωνισμό ενός μηνίσκου. Εκτός αυτού πρότεινε και τον τετραγωνισμό τριών άλλων μηνίσκων, στηριγμένος στην άποψη ότι όλοι οι μηνίσκοι των κανονικών πολυγώνων τετραγωνίζονται (Σιμπλίκιος).
Αυτός μάλλον θεώρησε όλους τους κύκλους ως όμοια σχήματα και πρότεινε δύο περίφημα θεωρήματα γι' αυτούς, τα παρακάτω:
(1) "Τα εμβαδά των κύκλων είναι ανάλογα των τετραγώνων των διαμέτρων τους" (Στοιχεία 2/ΧΙΙ) (Σιμπλίκιος). (Το πρώτο θεώρημα απειροστικού λογισμού).
(2) "Τα εμβαδά ομοίων κυκλικών τμημάτων (με ίσες επίκεντρες γωνίες) είναι ανάλογα των τετραγώνων των χορδών τους" (Εύδημος).
Οι μαθηματικές του αρχές ήταν Πυθαγόρειες, και είναι πιθανό για τη γεωμετρία εκείνων να είχε πληροφορίες από δημοσιεύσεις του Φιλολάου (440 π.Χ.) ή του αρχαιότερου 'Iππασου (~510 π.Χ.). Το σύνολο της μαθηματικής του δράσης του χάρισε τον τίτλο του "Ευφυούς" γεωμέτρη, ο οποίος με το πρωτοπόρο έργο του, ώθησε την ελληνική γεωμετρία σε νέες κατακτήσεις.
Οι μηνίσκοι του Ιπποκράτη
Ο μεγάλος γεωμέτρης Ιπποκράτης ο Χίος, στην προσπάθεια του να τετραγωνίσει τον κύκλο, πέτυχε τον τετραγωνισμό των μηνίσκων.
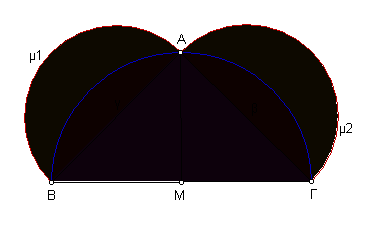
Στο ορθογώνιο και ισοσκελές τρίγωνο ΑΒΓ (ΑΒ=ΑΓ), κατασκεύασε τα ημικύκλια με διαμέτρους ΒΓ, ΑΒ και ΑΓ. Μεταξύ των τριών ημικυκλίων σχηματίστηκαν οι ίσοι μηνίσκοι μ1 και μ2 για τους οποίους απέδειξε ότι:
Εμβαδόν μηνίσκου (μ1) + Εμβαδόν μηνίσκου (μ2) = Εμβαδόν τριγώνου ΑΒΓ
Επι πλέον ήταν γνωστή η κατασκευή ενός τετραγώνου με εμβαδόν ίσο με το εμβαδόν του τριγώνου ΑΒΓ

Εμβαδόν τριγώνου ΑΒΓ = Εμβαδόν τετραγώνου ΑΜΓΜ΄ οπότε:
Εμβαδόν μηνίσκου (μ1) + Εμβαδόν μηνίσκου (μ2) = Εμβαδόν τετραγώνου ΑΜΓΜ΄
Βιβλιογραφια - Πηγες
[1] "Wikipedia"
[2] "TeleMath"
[3] "MathP"
Σωτήρης Χ. Γκουντουβάς, "Γεωμετρικές Διαδρομές", Αθήνα 2015
Γιάννης Χριστιανίδης, "Θέματα από την ιστορία των Μαθηματικών", ΠΕΚ, Ηράκλειο 2003
Άπαντα Αρχαίων Ελλήνων Συγγραφέων, Εκδόσεις ΠΑΠΥΡΟΣ, Αθήνα 1965
Πρόκλος ο Διάδοχος, "Σχόλια στο 1ο βιβλίο των Στοιχείων του Ευκλείδη", Λειψία 1897
Thomas Heath, "Ιστορία των Ελληνικών Μαθηματικών", ΚΕΠΕΚ, Αθήνα 2001
Β. L. Van der Waerden, "H αφύπνιση της επιστήμης", ΠΕΚ, Ηράκλειο 2003













