Θεοδωρος ο Κυρηναιος
Ο Θεόδωρος ο Κυρηναίος (~465-398 π.Χ) ήταν αρχαίος Έλληνας μαθηματικός και φιλόσοφος.
Βιογραφικά στοιχεία
Ο Θεόδωρος γεννήθηκε περίπου το 465 π.Χ στην Κυρήνη, μια ελληνική αποικία στην ανατολική πλευρά του κόλπου της Σύρτης στη σημερινή Λιβύη. Τα νεανικά του χρόνια πρέπει να θήτευσε στη Σχολή των Πυθαγορείων, στον Κρότωνα της Κάτω Ιταλίας.
Εκεί εντρύφησε στις μελέτες των Πυθαγορείων για την ασυμμετρία, τις οποίες και προήγαγε. Επίσης αναφέρεται ότι ήταν και μαθητής του Πρωταγόρα. Μετά τη διάλυση της Σχολής των Πυθαγορείων επέστρεψε στην Κυρήνη και πρέπει να άνοιξε δική του φιλοσοφική σχολή. Εκεί γνώρισε τον Πλάτωνα, που είχε επισκεφθεί την Κυρήνη και ο οποίος έγινε μαθητής του Θεόδωρου.
Στη συνέχεια ο Θεόδωρος εγκαταστάθηκε στην Αθήνα, όπου έζησε για πολλά χρόνια, και είχε για μαθητή του εκτός από τον Πλάτωνα και τους Θεαίτητο και Λεωδάμαντα.
Εκτός από τα μαθηματικά ασχολήθηκε με τη φιλοσοφία, την αστρονομία και τη μουσική (Heath, Thomas (1921), σελ. 584).
Ο Θεόδωρος ήταν από τους κύριους εκπροσώπους της Κυρηναϊκής σχολής της ηθικής φιλοσοφίας. Πίστευε ότι η ευχαρίστηση και ο πόνος δεν είναι ούτε καλό ούτε κακό. Επίσης ότι η ευθυμία και η φρόνηση είναι επαρκείς για την ευτυχία.
Ο Θεόδωρος πέθανε το 398 π.Χ, μάλλον, στην πατρίδα του την Κυρήνη.
Το μαθηματικό του έργο
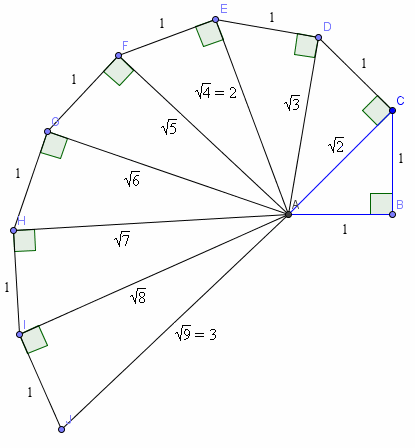
Οι κύριες μελέτες του Θεόδωρου αφορούν την ασυμμετρία (αρρητότητα). Απο τον πλατωνικό διάλογο Θεαίτητος γνωρίζουμε ότι ο Θεόδωρος είχε αποδείξει την αρρητότητα των τετραγωνικών ριζών από 3 έως 17. Ο διάλογος έχει ως εξής:
«Περί δυνάμεων τι ημίν Θεόδωρος όδε έγραφε, της τε τρίποδος περί και πεντέποδος, αποφαίνων ότι μήκει ού ξύμμετροι τη ποδιαία, και ούτω κατά μίαν εκάστη προαιρούμενος μέχρι της επτακαιδεκάποδος, εν δε ταύτη πως ενέσχετο. Ημίν ουν εισήλθε τι τοιούτον, επειδή άπειροι το πλήθος αι δυνάμεις εφαίνοντο, πειραθήναι ξυλλαβείν εις εν, ότω πάσας ταύτας προσαγορεύσομεν τας δυνάμεις.» (Θεαίτητος 147 D) - (Άπαντα Αρχαίων Ελλήνων (1975), σελ. 158).
Στον Σ. Γκουντουβάς (2009), σελ.66, διαβάζουμε:
Ο Θεόδωρος από ’δω έγραφε σχετικά με τις δυνάμεις (ρίζες) συμπεραίνοντας ότι οι δυνάμεις (ρίζες) των τριών ποδών και των πέντε ποδών δεν είναι σύμμετρες με τη δύναμη του ενός ποδός και με αυτόν τον τρόπο εξακολούθησε τη μία δύναμη μετά την άλλη και έφτασε μέχρι τη δεκάτη εβδόμη και σε αυτή φάνηκε να σταμάτησε. Σε μας λοιπόν ήρθε η ιδέα, επειδή άπειρες οι δυνάμεις (ρίζες) στο πλήθος φαινόταν, να τις συγκεντρώσουμε σε μία μέθοδο και έτσι όλες αυτές να τις χειριζόμαστε.
Με σύγχρονη ορολογία ο Θεόδωρος απέδειξε ότι οι τετραγωνικές ρίζες των αριθμών από 3 έως 17 είναι άρρητοι αριθμοί χρησιμοποιώντας σε κάθε περίπτωση διαφορετική μέθοδο και εκεί σταμάτησε. Τότε σκέφθηκαν να ενοποιήσουν τις επιμέρους μεθόδους σε μία για να αποδεικνύουν την αρρητότητα για κάθε περίπτωση. Το κείμενο δεν διευκρινίζει αν αποδείχθηκε η αρρητότητα του 17.
Οι περισσότεροι ιστορικοί των μαθηματικών ισχυρίζονται ότι απέδειξε και το 17, ενώ κάποιοι άλλοι ότι δεν απέδειξε το 17. Επίσης το κείμενο δεν μας διαφωτίζει για το ποια ήταν η απόδειξη που χρησιμοποιήθηκε για κάθε περίπτωση, ούτε για την ενοποιημένη μέθοδο. Επίσης δεν μας πληροφορεί για ποιο λόγο σταμάτησαν στο 17.
Αν λοιπόν είχε αποδειχθεί η αρρητότητα για το 17 τότε θα είχε αποδειχθεί και για το 18 αφού 18=2x9. Αν δεν είχε αποδειχθεί η αρρητότητα για το 17 τότε θα είχαν αποδείξει μέχρι και το 15, αφού για το 16 έχουμε ότι 16=4^2. Για το χωρίο αυτό έχουν γίνει πάρα πολλές μελέτες για να διευκρινιστούν οι πτυχές των θεμάτων που θίγει. Έχουν γίνει ανακατασκευές των πιθανών αποδείξεων καθώς και εξηγήσεις για το σταμάτημα στο 17.
Αυτό το χωρίο λοιπόν μας πληροφορεί για την αναμφισβήτητη πρόοδο που είχε επιτελεστεί σχετικά με την ασυμμετρία με πρωταγωνιστή τον Θεόδωρο, σε σχέση με τους Πυθαγορείους ( Σ. Γκουντουβάς (2015), σελ.32-33).
Πηγες
"School of Mathematics and Statistics University of St Andrews, Scotland " by J J O'Connor and E F Robertson
I Bulmer-Thomas, Biography in Dictionary of Scientific Biography (New York 1970-1990).
B Artmann, A proof for Theodorus' theorem by drawing diagrams, J. Geom. 49 (1-2) (1994), 3-35.
M S Brown, Theaetetus : Knowledge as Continued Learning, Journal of the History of Philosophy 7 (1969), 359-379.
L Giacardi, On Theodorus of Cyrene's problem, Arch. Internat. Hist. Sci. 27 (101) (1977), 231-236.
T L Heath, A History of Greek Mathematics I (Oxford, 1921), 203-204, 209-212.
R L McCabe, Theodorus' irrationality proofs, Math. Mag. 49 (4) (1976), 201-203.
A Wasserstein, Theaetetus and the History of the Theory of Numbers, Classical Quarterly 8 (1958), 165-179.
Άπαντα Αρχαίων Ελλήνων Συγγραφέων, Διάλογοι Πλάτωνος, Αθήνα 1975, Εκδόσεις Πάπυρος.
Σωτήρης Χ. Γκουντουβάς, "Το νόημα της κατασκευής στην πορεία εξέλιξης της Γεωμετρίας", Διπλωματική Διατριβή, ΕΚΠΑ, Αθήνα 2009
Σωτήρης Χ. Γκουντουβάς, "Γεωμετρικές Διαδρομές", αυτοέκδοση, Αθήνα 2015
Thomas Heath, "Ιστορία των Ελληνικών Μαθηματικών", ΚΕΠΕΚ, Αθήνα 2001
Β. L. Van der Waerden, "H αφύπνιση της επιστήμης", ΠΕΚ, Ηράκλειο 2003
Η εφαρμογη μας για το κινητο σου
Κατέβασε και εσύ την εφαρμογή μας για το κινητό σου "Ancient Greece Reloaded"